Kwantowa odległość Wassersteina oparta na optymalizacji stanów rozdzielonych

Opublikowane ponownie przez Plato

Obserwuje: 0

Geza Tóth^1,2,3,4,5 i Józsefa Pitrika^5,6,7

¹Fizyka teoretyczna, Uniwersytet Kraju Basków UPV/EHU, ES-48080 Bilbao, Hiszpania
²EHU Quantum Center, Uniwersytet Kraju Basków UPV/EHU, Barrio Sarriena s/n, ES-48940 Leioa, Biskajska, Hiszpania
³Międzynarodowe Centrum Fizyki Donostia (DIPC), ES-20080 San Sebastián, Hiszpania
⁴IKERBASQUE, Baskijska Fundacja Nauki, ES-48011 Bilbao, Hiszpania
⁵Institute for Solid State Physics and Optics, Wigner Research Centre for Physics, HU-1525 Budapeszt, Węgry
⁶Instytut Matematyki Alfréda Rényi, Reáltanoda u. 13-15., HU-1053 Budapeszt, Węgry
⁷Katedra Analiz i Badań Operacyjnych, Instytut Matematyki, Uniwersytet Techniczno-Ekonomiczny w Budapeszcie, Müegyetem rkp. 3., HU-1111 Budapeszt, Węgry

Czy ten artykuł jest interesujący czy chcesz dyskutować? Napisz lub zostaw komentarz do SciRate.

Abstrakcyjny

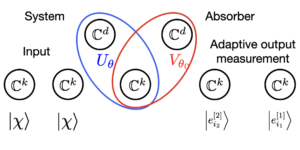
Definiujemy kwantową odległość Wassersteina w taki sposób, że optymalizację sprzężenia przeprowadza się w odniesieniu do dwudzielnych stanów rozdzielnych, a nie ogólnie do dwudzielnych stanów kwantowych, i badamy jej właściwości. Co zaskakujące, okazuje się, że dystans własny jest powiązany z kwantową informacją Fishera. Przedstawiamy mapę transportową odpowiadającą optymalnemu dwustronnemu stanowi separacyjnemu. Omawiamy, w jaki sposób wprowadzona kwantowa odległość Wassersteina jest powiązana z kryteriami wykrywającymi splątanie kwantowe. Definiujemy wielkości wariancyjne, które można otrzymać z kwantowej odległości Wassersteina, zastępując minimalizację stanów kwantowych maksymalizacją. Rozszerzamy nasze wyniki na rodzinę uogólnionych ilości informacji kwantowej Fishera.

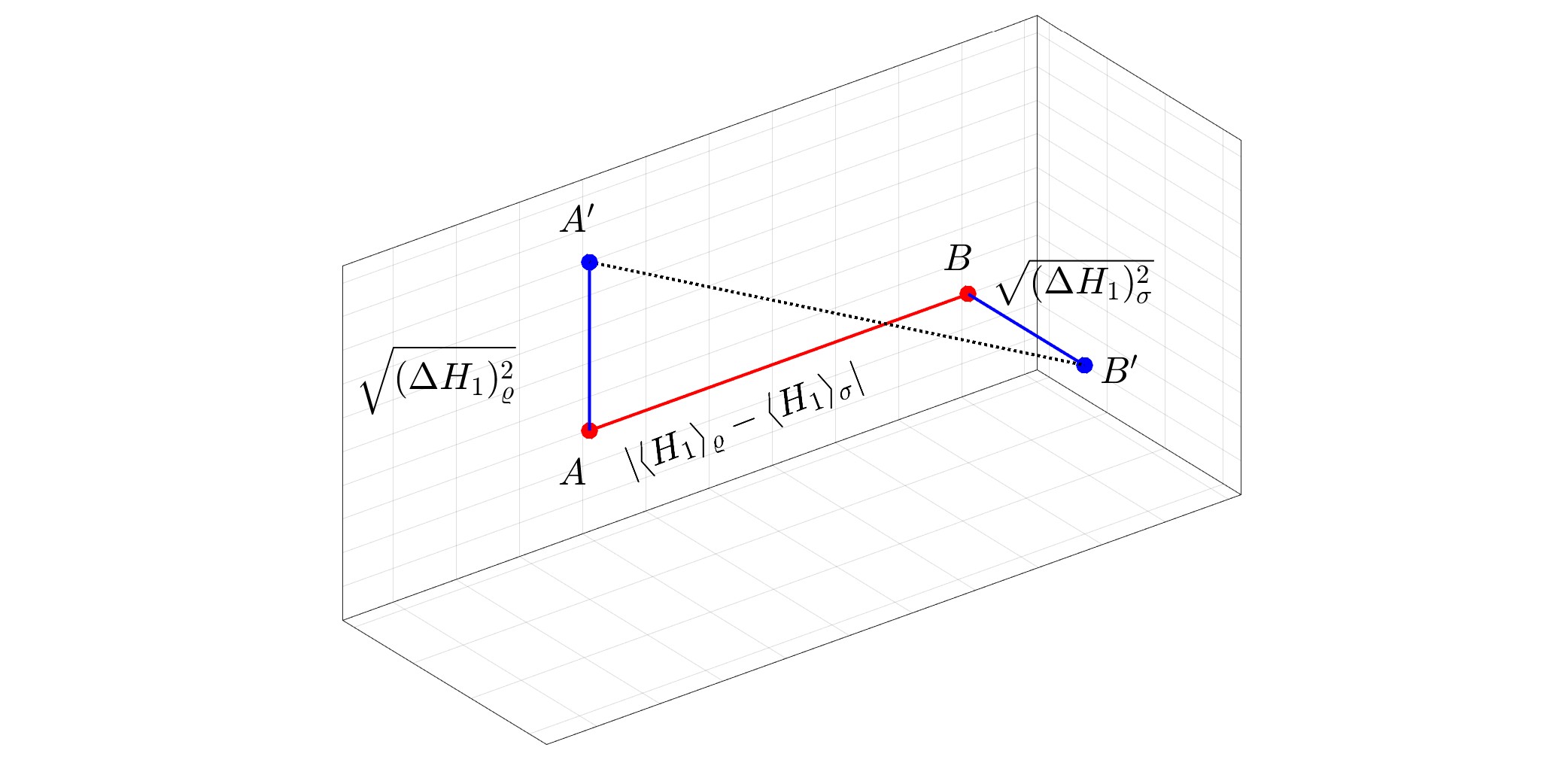
Wyróżniony obraz: Geometryczna reprezentacja kwantowej odległości Wassersteina pomiędzy stanem czystym $varrho$ i stanem mieszanym $sigma$ dla $N=1.$ Kwantowa odległość Wassersteina jest równa $1/sqrt2$ razy zwykła odległość euklidesowa pomiędzy $A'$ i $B'.$

Popularne podsumowanie

W życiu codziennym odległość dwóch miast mówi nam, ile kilometrów musimy przejechać z jednego do drugiego. Można także scharakteryzować, jak łatwo możemy dostać się z jednego miasta do drugiego, mierząc zużycie paliwa podczas naszej podróży. To drugie rozwiązanie ma charakter bardziej informacyjny w tym sensie, że odzwierciedla koszt podróży w powiązaniu z topografią drogi, tj. jest wrażliwe na podstawowy wskaźnik. Następnie wyobraźmy sobie, że musimy przenieść hałdę piasku z jednego miejsca na drugie, a nowa hałda może mieć inną formę. W tym przypadku ponownie możemy scharakteryzować wysiłek związany z przemieszczaniem piasku kosztem transportu.

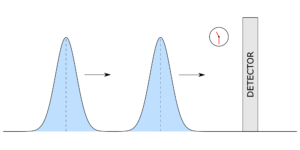
Odległości odgrywają kluczową rolę w matematyce, fizyce i inżynierii. Podstawowym problemem prawdopodobieństwa i statystyki jest znalezienie użytecznych miar odległości między dwoma rozkładami prawdopodobieństwa. Niestety, wiele pojęć odległości między rozkładami prawdopodobieństwa, powiedzmy p(x) i q(x), jest maksymalnych, jeśli nie nakładają się na siebie, tj. jedno ma zawsze wartość zero, gdy drugie jest niezerowe. Jest to niepraktyczne w wielu zastosowaniach. Przykładowo, wracając do analogii z piaskiem, dwie nienakładające się na siebie stosy piasku wydają się być jednakowo oddalone od siebie, niezależnie od tego, czy ich odległość wynosi 10 czy 100 km. Teoria transportu optymalnego jest sposobem na skonstruowanie alternatywnego pojęcia odległości między rozkładami prawdopodobieństwa, tzw. odległości Wassersteina. Może być niemaksymalny, nawet jeśli rozkłady nie nakładają się na siebie, jest wrażliwy na podstawową metrykę (tj. koszt transportu) i zasadniczo wyraża wysiłek, jakiego potrzebujemy, aby przenieść się jeden do drugiego, jakby były piaszczystymi wzgórzami.

Niedawno zdefiniowano kwantową odległość Wassersteina, uogólniając klasyczną odległość Wassersteina. Opiera się na minimalizacji funkcji kosztu po stanach kwantowych dwudzielnego układu kwantowego. Ma ona właściwość analogiczną do wspomnianej powyżej w świecie kwantowym. Może ona być niemaksymalna dla stanów ortogonalnych, co jest przydatne na przykład wtedy, gdy musimy nauczyć algorytm danych kwantowych.

Jak można się spodziewać, kwantowa odległość Wassersteina również ma właściwości bardzo odmienne od jej klasycznego odpowiednika. Na przykład, gdy mierzymy odległość stanu kwantowego od niego samego, może ona być różna od zera. Chociaż jest to już zagadkowe, odkryto również, że dystans własny jest powiązany z informacją o skośności Wignera-Yanase'a, wprowadzoną w 1963 roku przez laureata Nagrody Nobla EP Wignera, który wniósł istotny wkład w podstawy fizyki kwantowej i MM Yanase.

W naszym artykule patrzymy na to tajemnicze odkrycie z jeszcze innej strony. Wspomnianą powyżej minimalizację ograniczamy do tzw. stanów separowalnych. Są to stany kwantowe, w których nie występuje splątanie. Odkryliśmy, że dystans własny staje się kwantową informacją Fishera, wielkością centralną w metrologii kwantowej i teorii estymacji kwantowej, pojawiającą się na przykład w słynnej granicy Cramera-Rao. Badając właściwości takiej odległości Wassersteina, nasza praca toruje drogę do powiązania teorii kwantowej odległości Wassersteina z teorią splątania kwantowego.

► Dane BibTeX

@article{Toth2023quantumwasserstein, doi = {10.22331/q-2023-10-16-1143}, url = {https://doi.org/10.22331/q-2023-10-16-1143}, tytuł = {Quantum { Odległość W}assersteina oparta na optymalizacji po stanach rozdzielnych}, autor = {T{'{o}}th, G{'{e}}za i Pitrik, J{'{o}}zsef}, dziennik = {{ Quantum}}, issn = {2521-327X}, wydawca = {{Verein zur F{„{o}}rderung des Open Access Publizierens in den Quantenwissenschaften}}, tom = {7}, strony = {1143}, miesiąc = październik, rok = {2023> }

► Referencje

[1] G. Monge’a. „Mémoire sur la théory des déblais et des remblais”. Mémoires de l'Académie Royale de Sciences de Paris (1781).

[2] L.Kantorowicz. „O przemieszczeniu mas”. Nauka o zarządzaniu 5, 1–4 (1958). adres URL: http:///www.jstor.org/stable/2626967.
http: // www.jstor.org/ stabilny / 2626967

[3] Emmanuela Boissarda, Thibauta Le Gouica i Jeana-Michela Loubesa. „Szacunek szablonu dystrybucji za pomocą metryk Wassersteina”. Bernoulli 21, 740–759 (2015).
https:///doi.org/10.3150/13-bej585

[4] Olega Butkowskiego. „Subgeometryczne współczynniki zbieżności procesów Markowa w metryce Wassersteina”. Anna. Aplikacja Prawdopodobne. 24, 526–552 (2014).
https:///doi.org/10.1214/13-AAP922

[5] M. Hairer, J.-C. Mattingly i M. Scheutzow. „Sprzężenie asymptotyczne i ogólna postać twierdzenia Harrisa z zastosowaniami do stochastycznych równań opóźnienia”. Prawdopodobne. Teoria dot. Pola 149, 223–259 (2011).
https://doi.org/10.1007/s00440-009-0250-6

[6] M. Hairer i JC Mattingly. „Przerwy widmowe w odległościach Wassersteina i 2D stochastyczne równania Naviera-Stokesa”. Anna. Prawdopodobne. 36, 2050–2091 (2008).
https:///doi.org/10.1214/08-AOP392

[7] A. Figalli, F. Maggi i A. Pratelli. „Podejście transportu masowego do ilościowych nierówności izoperymetrycznych”. Wynaleźć. Matematyka. 182, 167–211. (2010).
https: / / doi.org/ 10.1007 / s00222-010-0261-z

[8] A. Figalli i F. Maggi. „O kształcie kropli cieczy i kryształów w reżimie małych mas”. Łuk. Racjonować. Mech. Analny. 201, 143–207 (2011).
https: / / doi.org/ 10.1007 / s00205-010-0383-x

[9] J. Lotta i C. Villaniego. „Krzywizna Ricciego dla przestrzeni miar metrycznych poprzez optymalny transport”. Anna. matematyki. 169 (3), 903–991 (2009).
https:///doi.org/10.48550/arXiv.math/0412127

[10] Max-K. von Renesse’a i Karla-Theodora Sturma. „Nierówności transportowe, szacunki gradientów, entropia i krzywizna Ricciego”. Komunikator Czysta aplikacja Matematyka. 58, 923–940 (2005).
https: / / doi.org/ 10.1002 / cpa.20060

[11] Karla-Theodora Sturma. „O geometrii metrycznych przestrzeni miar I”. Akta matematyki. 196, 65–131 (2006).
https://doi.org/10.1007/s11511-006-0002-8

[12] Karla-Theodora Sturma. „O geometrii metrycznych przestrzeni miar II”. Akta matematyki. 196, 133–177 (2006).
https://doi.org/10.1007/s11511-006-0003-7

[13] Benoı̂t Kloeckner. „Badanie geometryczne przestrzeni Wassersteina: przestrzenie euklidesowe”. Annali della Scuola Normale Superiore di Pisa – Classe di Scienze, Scuola Normale Superiore 2010 IX (2), 297–323 (2010).
https: // doi.org/ 10.2422 / 2036-2145.2010.2.03

[14] György Pál Gehér, Tamás Titkos i Dániel Virosztek. „O izometrycznych osadzaniach przestrzeni Wassersteina – przypadek dyskretny”. J. Matematyka. Analny. Aplikacja 480, 123435 (2019).
https:///doi.org/10.1016/j.jmaa.2019.123435

[15] György Pál Gehér, T. Titkos, Dániel Virosztek. „Badania izometryczne przestrzeni Wassersteina – linia rzeczywista”. Przeł. Amera. Matematyka. Towarzystwo 373, 5855–5883 (2020).
https:///doi.org/10.1090/tran/8113

[16] György Pál Gehér, Tamás Titkos i Dániel Virosztek. „Grupa izometryczna przestrzeni Wassersteina: przypadek Hilberta”. J. Londa. Matematyka. Towarzystwo 106, 3865–3894 (2022).
https:///doi.org/10.1112/jlms.12676

[17] György Pál Gehér, Tamás Titkos i Dániel Virosztek. „Sztywność izometryczna tori i kul Wassersteina”. Mathematika 69, 20–32 (2023).
https:///doi.org/10.1112/mtk.12174

[18] Gergely Kiss i Tamás Titkos. „Sztywność izometryczna przestrzeni Wassersteina: przypadek metryczny grafów”. Proc. Jestem. Matematyka. Towarzystwo 150, 4083–4097 (2022).
https:///doi.org/10.1090/proc/15977

[19] György Pál Gehér, Tamás Titkos i Dániel Virosztek. „O egzotycznym przepływie izometrii kwadratowej przestrzeni Wassersteina nad linią rzeczywistą”. Aplikacja algebry liniowej (2023).
https: / / doi.org/ 10.1016 / j.laa.2023.02.016

[20] S. Kolouri, S. R. Park i G. K. Rohde. „Transformata rozkładu skumulowanego Radona i jej zastosowanie do klasyfikacji obrazów”. IEEE Trans. Proces obrazu. 25, 920–934 (2016).
https:///doi.org/10.1109/TIP.2015.2509419

[21] W. Wang, D. Slepc̆ev, S. Basu, J. A. Ozolek i G. K. Rohde. „Liniowe optymalne ramy transportu do ilościowego określania i wizualizacji zmian w zestawach obrazów”. Wewnętrzne J. Oblicz. Wisz. 101, 254–269 (2013).
https: / / doi.org/ 10.1007 / s11263-012-0566-z

[22] S. Kolouri, S. Park, M. Thorpe, D. Slepc̆ev, G. K. Rohde. „Optymalny transport masy: przetwarzanie sygnałów i zastosowania uczenia maszynowego”. Magazyn IEEE Signal Processing 34, 43–59 (2017).
https: // doi.org/ 10.1109 / MSP.2017.2695801

[23] A. Gramfort, G. Peyré i M. Cuturi. „Szybkie optymalne uśrednianie danych neuroobrazowych w transporcie”. Przetwarzanie informacji w obrazowaniu medycznym. IPMI 2015. Notatki z wykładów z informatyki 9123, 261–272 (2015).
https://doi.org/10.1007/978-3-319-19992-4_20

[24] Z. Su, W. Zeng, Y. Wang, Z. L. Lu i X. Gu. „Klasyfikacja kształtu za pomocą odległości Wassersteina do analizy morfometrii mózgu”. Przetwarzanie informacji w obrazowaniu medycznym. IPMI 2015. Notatki z wykładów z informatyki 24, 411–423 (2015).
https://doi.org/10.1007/978-3-319-19992-4_32

[25] Martin Arjovsky, Soumith Chintala i Léon Bottou. „Generatywne sieci przeciwstawne Wassersteina”. W: Doina Precup i Yee Whye Teh, redaktorzy, Materiały z 34. Międzynarodowej Konferencji na temat uczenia maszynowego. Tom 70 Proceedings of Machine Learning Research, strony 214–223. PMLR (2017). arXiv:1701.07875.
arXiv: 1701.07875

[26] T. A. El Moselhy i Y. M. Marzouk. „Wnioskowanie bayesowskie z optymalnymi mapami”. J. Oblicz. Fiz. 231, 7815–7850 (2012).
https:///doi.org/10.1016/j.jcp.2012.07.022

[27] Gabriel Peyré i Marco Cuturi. „Obliczeniowy transport optymalny: z zastosowaniami do nauki o danych”. Znaleziony. Trendy Uczenie maszynowe. 11, 355–602 (2019).
https: / / doi.org/ 10.1561 / 2200000073

[28] Charlie Frogner, Chiyuan Zhang, Hossein Mobahi, Mauricio Araya i Tomaso A Poggio. „Uczenie się ze stratą Wassersteina”. W: C. Cortes, N. Lawrence, D. Lee, M. Sugiyama i R. Garnett, redaktorzy, Advances in Neural Information Processing Systems. Tom 28. Curran Associates, Inc. (2015). arXiv:1506.05439.
arXiv: 1506.05439

[29] A. Ramdas, N. G. Trillos i M. Cuturi. „O testowaniu dwóch próbek Wassersteina i pokrewnych rodzinach testów nieparametrycznych”. Entropia 19, 47. (2017).
https: / / doi.org/ 10.3390 / e19020047

[30] S. Srivastava, C. Li i DB Dunson. „Skalowalne Bayesa poprzez Barycenter w przestrzeni Wassersteina”. J. Mach. Uczyć się. Rozdzielczość 19, 1–35 (2018). arXiv:1508.05880.
arXiv: 1508.05880

[31] Karol Życzkowski i Wojeciech Słomczyński. „Odległość Monge’a między stanami kwantowymi”. J.Fiz. O: Matematyka. Gen. 31, 9095–9104 (1998).
https://doi.org/10.1088/0305-4470/31/45/009

[32] Karol Życzkowski i Wojciech Słomczyński. „Metryka Monge’a na kuli i geometrii stanów kwantowych”. J.Fiz. O: Matematyka. Gen. 34, 6689–6722 (2001).
https://doi.org/10.1088/0305-4470/34/34/311

[33] Ingemar Bengtsson i Karol Życzkowski. „Geometria stanów kwantowych: wprowadzenie do splątania kwantowego”. Wydawnictwo Uniwersytetu Cambridge. (2006).
https: / / doi.org/ 10.1017 / CBO9780511535048

[34] P. Biane i D. Voiculescu. „Swobodny analog prawdopodobieństwa metryki Wassersteina w przestrzeni stanów śladowych”. GAFA, Geom. Funkcja. Analny. 11, 1125–1138 (2001).
https://doi.org/10.1007/s00039-001-8226-4

[35] Eric A. Carlen i Jan Maas. „Analog metryki 2-Wassersteina w prawdopodobieństwie nieprzemiennym, zgodnie z którym fermionowe równanie Fokkera-Plancka jest gradientowym przepływem entropii”. komuna. Matematyka. Fiz. 331, 887–926 (2014).
https://doi.org/10.1007/s00220-014-2124-8

[36] Eric A. Carlen i Jan Maas. „Nierówności przepływu gradientu i entropii dla kwantowych półgrup Markowa ze szczegółowym bilansem”. J. Funkt. Analny. 273, 1810–1869 (2017).
https: / / doi.org/ 10.1016 / j.jfa.2017.05.003

[37] Eric A. Carlen i Jan Maas. „Rachunek nieprzemienny, transport optymalny i nierówności funkcjonalne w rozpraszających układach kwantowych”. J.Stat. Fiz. 178, 319–378 (2020).
https: / / doi.org/ 10.1007 / s10955-019-02434-w

[38] Nilanjana Datta i Cambyse Rouzé. „Koncentracja stanów kwantowych z kwantowych nierówności funkcjonalnych i kosztów transportu”. J. Matematyka. Fiz. 60, 012202 (2019).
https: / / doi.org/ 10.1063 / 1.5023210

[39] Nilanjana Datta i Cambyse Rouzé. „Powiązanie względnej entropii, optymalnego transportu i informacji Fishera: kwantowa nierówność HWI”. Anna. Henri Poincaré 21, 2115–2150 (2020).
https://doi.org/10.1007/s00023-020-00891-8

[40] François Golse, Clément Mouhot i Thierry Paul. „O polu średnim i klasycznych granicach mechaniki kwantowej”. komuna. Matematyka. Fiz. 343, 165–205 (2016).
https://doi.org/10.1007/s00220-015-2485-7

[41] Francois Golse i Thierry Paul. „Równanie Schrödingera w układzie pola średniego i reżimie półklasycznym”. Łuk. Racjonować. Mech. Analny. 223, 57–94 (2017).
https: / / doi.org/ 10.1007 / s00205-016-1031-x

[42] Francois Golse i Thierry Paul. „Pakiety falowe i kwadratowa odległość Monge-Kantorovicha w mechanice kwantowej”. Obliczenia Comptes Rendus. 356, 177–197 (2018).
https:///doi.org/10.1016/j.crma.2017.12.007

[43] François Golse. „Zagadnienie ciała kwantowego $N$ w układzie pola średniego i reżimie półklasycznym”. Fil. Przeł. R. Soc. A 376, 20170229 (2018).
https: / / doi.org/ 10.1098 / rsta.2017.0229

[44] E. Caglioti, F. Golse i T. Paul. „Transport optymalny kwantowo jest tańszy”. J.Stat. Fiz. 181, 149–162 (2020).
https://doi.org/10.1007/s10955-020-02571-7

[45] Emanuele Caglioti, François Golse i Thierry Paul. „W kierunku optymalnego transportu dla gęstości kwantowych”. arXiv:2101.03256 (2021).
https:///doi.org/10.48550/arXiv.2101.03256
arXiv: 2101.03256

[46] Giacomo De Palma i Dario Trevisan. „Kwantowy optymalny transport kanałami kwantowymi”. Anna. Henri Poincaré 22, 3199–3234 (2021).
https://doi.org/10.1007/s00023-021-01042-3

[47] Giacomo De Palma, Milad Marvian, Dario Trevisan i Seth Lloyd. „Kwantowa odległość Wassersteina rzędu 1”. IEEE Trans. Inf. Teoria 67, 6627–6643 (2021).
https: / / doi.org/ 10.1109 / TIT.2021.3076442

[48] Shmuel Friedland, Michał Eckstein, Sam Cole i Karol Życzkowski. „Kwantowy problem Monge’a – Kantorowicza i odległość transportu pomiędzy macierzami gęstości”. Fiz. Wielebny Lett. 129, 110402 (2022).
https: / / doi.org/ 10.1103 / PhysRevLett.129.110402

[49] Sam Cole, Michał Eckstein, Shmuel Friedland i Karol Życzkowski. „Transport optymalny kwantowo”. arXiv:2105.06922 (2021).
https:///doi.org/10.48550/arXiv.2105.06922
arXiv: 2105.06922

[50] R. Bistroń, M. Eckstein i K. Życzkowski. „Monotoniczność kwantowej odległości 2-Wassersteina”. J.Fiz. O: Matematyka. Teoria. 56, 095301 (2023).
https://doi.org/10.1088/1751-8121/acb9c8

[51] György Pál Gehér, József Pitrik, Tamás Titkos i Dániel Virosztek. „Kwantowe izometrie Wassersteina w przestrzeni stanów kubitu”. J. Matematyka. Analny. Aplikacja 522, 126955 (2023).
https:///doi.org/10.1016/j.jmaa.2022.126955

[52] Lu Li, Kaifeng Bu, Dax Enshan Koh, Arthur Jaffe i Seth Lloyd. „Złożoność Wassersteina obwodów kwantowych”. arXiv: 2208.06306 (2022).
https:///doi.org/10.48550/arXiv.2208.06306

[53] Bobak Toussi Kiani, Giacomo De Palma, Milad Marvian, Zi-Wen Liu i Seth Lloyd. „Nauka danych kwantowych za pomocą odległości kwantowego poruszacza ziemi”. Nauka kwantowa. Techn. 7, 045002 (2022).
https://doi.org/10.1088/2058-9565/ac79c9

[54] EP Wigner i Mutsuo M. Yanase. „Zawartość informacyjna dystrybucji”. Proc. Natl. Acad. Nauka. USA 49, 910–918 (1963).
https: / / doi.org/ 10.1073 / pnas.49.6.910

[55] Ryszard Horodecki, Paweł Horodecki, Michał Horodecki i Karol Horodecki. "Splątanie kwantowe". Wielebny Mod. fizyka 81, 865–942 (2009).
https: / / doi.org/ 10.1103 / RevModPhys.81.865

[56] Otfried Gühne i Géza Tóth. „Wykrywanie splątania”. fizyka Rep. 474, 1–75 (2009).
https: / / doi.org/ 10.1016 / j.physrep.2009.02.004

[57] Nicolai Friis, Giuseppe Vitagliano, Mehul Malik i Marcus Huber. „Certyfikat splątania od teorii do eksperymentu”. Nat. Wielebny Fiz. 1, 72–87 (2019).
https://doi.org/10.1038/s42254-018-0003-5

[58] Vittorio Giovannetti, Seth Lloyd i Lorenzo Maccone. „Pomiary wzmocnione kwantowo: pokonanie standardowego limitu kwantowego”. Nauka 306, 1330–1336 (2004).
https: / / doi.org/ 10.1126 / science.1104149

[59] Matteo G. A. Paryż. „Estymacja kwantowa dla technologii kwantowej”. Wewnętrzne J. Quant. Inf. 07, 125–137 (2009).
https: / / doi.org/ 10.1142 / S0219749909004839

[60] Rafał Demkowicz-Dobrzański, Marcin Jarzyna i Jan Kołodyński. „Rozdział czwarty – Granice kwantowe w interferometrii optycznej”. Wałówka. Optyka 60, 345 – 435 (2015). arXiv:1405.7703.
https: / / doi.org/ 10.1016 / bs.po.2015.02.003
arXiv: 1405.7703

[61] Luca Pezze i Augusto Smerzi. „Kwantowa teoria estymacji fazowej”. w G.M. Tino i M.A. Kasevich, redaktorzy, Atom Interferometry (Proc. Int. School of Physics „Enrico Fermi”, kurs 188, Varenna). Strony 691–741. IOS Press, Amsterdam (2014). arXiv:1411.5164.
arXiv: 1411.5164

[62] Géza Tóth i Dénes Petz. „Ekstremalne właściwości wariancji i kwantowa informacja Fishera”. Fiz. Rev. A 87, 032324 (2013).
https: / / doi.org/ 10.1103 / PhysRevA.87.032324

[63] Sixia Yu. „Informacja Fishera kwantowego jako wypukły dach wariancji”. arXiv:1302.5311 (2013).
https:///doi.org/10.48550/arXiv.1302.5311
arXiv: 1302.5311

[64] Géza Tóth i Florian Fröwis. „Związki niepewności z wariancją i kwantową informacją Fishera na podstawie rozkładów wypukłych macierzy gęstości”. Fiz. Rev. Research 4, 013075 (2022).
https: / / doi.org/ 10.1103 / PhysRevResearch.4.013075

[65] Shao-Hen Chiew i Manuel Gessner. „Poprawa relacji niepewności sumy z kwantową informacją Fishera”. Fiz. Rev. Research 4, 013076 (2022).
https: / / doi.org/ 10.1103 / PhysRevResearch.4.013076

[66] C. W. Helstrom. „Kwantowa teoria detekcji i estymacji”. Prasa Akademicka, Nowy Jork. (1976). adres URL: www.elsevier.com/books/quantum-detection-and-estimation-theory/helstrom/978-0-12-340050-5.
https://www.elsevier.com/books/quantum-detection-and-estimation-theory/helstrom/978-0-12-340050-5

[67] A. S. Holevo. „Probabilistyczne i statystyczne aspekty teorii kwantowej”. Holandia Północna, Amsterdam. (1982).

[68] Samuel L. Braunstein i Carlton M. Caves. „Odległość statystyczna i geometria stanów kwantowych”. fizyka Wielebny Lett. 72, 3439-3443 (1994).
https: / / doi.org/ 10.1103 / PhysRevLett.72.3439

[69] Samuel L. Braunstein, Carlton M. Caves i Gerard J. Milburn. „Uogólnione relacje niepewności: teoria, przykłady i niezmienność Lorentza”. Anna. Fiz. 247, 135–173 (1996).
https: / / doi.org/ 10.1006 / aphy.1996.0040

[70] Dénes Petz. „Kwantowa teoria informacji i statystyka kwantowa”. Springera, Berlina, Heilderberga. (2008).
https://doi.org/10.1007/978-3-540-74636-2

[71] Géza Tóth i Iagoba Apellaniz. „Metrologia kwantowa z perspektywy informatyki kwantowej”. J. Fiz. O: Matematyka. Teoria. 47, 424006 (2014).
https://doi.org/10.1088/1751-8113/47/42/424006

[72] Luca Pezzè, Augusto Smerzi, Markus K. Oberthaler, Roman Schmied i Philipp Treutlein. „Metrologia kwantowa z nieklasycznymi stanami zespołów atomowych”. Wielebny Mod. fizyka 90, 035005 (2018).
https: / / doi.org/ 10.1103 / RevModPhys.90.035005

[73] Marco Barbieriego. „Optyczna metrologia kwantowa”. PRX Quantum 3, 010202 (2022).
https: // doi.org/ 10.1103 / PRXQuantum.3.010202

[74] Zoltán Léka i Dénes Petz. „Niektóre rozkłady wariancji macierzy”. Prawdopodobne. Matematyka. Statystyk. 33, 191–199 (2013). arXiv:1408.2707.
arXiv: 1408.2707

[75] Dénes Petz i Dániel Virosztek. „Twierdzenie o charakterystyce wariancji macierzy”. Acta Sci. Matematyka. (Szeged) 80, 681–687 (2014).
https:///doi.org/10.14232/actasm-013-789-z

[76] Akio Fujiwara i Hiroshi Imai. „Wiązka światłowodowa na rozmaitościach kanałów kwantowych i jej zastosowanie do statystyki kwantowej”. J.Fiz. O: Matematyka. Teoria. 41, 255304 (2008).
https://doi.org/10.1088/1751-8113/41/25/255304

[77] B. M. Escher, R. L. de Matos Filho i L. Davidovich. „Ogólne ramy szacowania ostatecznej granicy precyzji w zaszumionej metrologii kwantowej”. Nat. Fiz. 7, 406–411 (2011).
https: / / doi.org/ 10.1038 / nphys1958

[78] Rafał Demkowicz-Dobrzański, Jan Kołodyński i Mădălin Guţă. „Nieuchwytna granica Heisenberga w metrologii wzmocnionej kwantowo”. Nat. komuna. 3, 1063 (2012).
https: / / doi.org/ 10.1038 / ncomms2067

[79] Iman Marvian. „Operacyjna interpretacja informacji rybaka kwantowego w termodynamice kwantowej”. Fiz. Wielebny Lett. 129, 190502 (2022).
https: / / doi.org/ 10.1103 / PhysRevLett.129.190502

[80] Reinharda F. Wernera. „Stany kwantowe z korelacjami Einsteina-Podolskiego-Rosena dopuszczające model ukrytych zmiennych”. Fiz. Rev. A 40, 4277–4281 (1989).
https: / / doi.org/ 10.1103 / PhysRevA.40.4277

[81] K. Eckert, J. Schliemann, D. Bruss i M. Lewenstein. „Kwantowe korelacje w układach nierozróżnialnych cząstek”. Anna. Fiz. 299, 88–127 (2002).
https: / / doi.org/ 10.1006 / aphy.2002.6268

[82] Tsubasa Ichikawa, Toshihiko Sasaki, Izumi Tsutsui i Nobuhiro Yonezawa. „Symetria wymiany i splątanie wieloczęściowe”. Fiz. Rev. A 78, 052105 (2008).
https: / / doi.org/ 10.1103 / PhysRevA.78.052105

[83] Paweł Horodecki. „Kryterium rozdzielności i nierozłączne stany mieszane z dodatnią transpozycją częściową”. Fiz. Łotysz. A 232, 333–339 (1997).
https://doi.org/10.1016/S0375-9601(97)00416-7

[84] Asher Peres. „Kryterium rozdzielności macierzy gęstości”. Fiz. Ks. 77, 1413-1415 (1996).
https: / / doi.org/ 10.1103 / PhysRevLett.77.1413

[85] Paweł Horodecki, Michał Horodecki i Ryszard Horodecki. „Można aktywować splątanie związane”. Fiz. Wielebny Lett. 82, 1056–1059 (1999).
https: / / doi.org/ 10.1103 / PhysRevLett.82.1056

[86] Géza Tóth i Tamás Vértesi. „Stany kwantowe z dodatnią transpozycją częściową są przydatne w metrologii”. Fiz. Wielebny Lett. 120, 020506 (2018).
https: / / doi.org/ 10.1103 / PhysRevLett.120.020506

[87] Scotta Hilla i Williama K. Woottersa. „Splątanie pary bitów kwantowych”. Fiz. Wielebny Lett. 78, 5022–5025 (1997).
https: / / doi.org/ 10.1103 / PhysRevLett.78.5022

[88] Williama K. Woottersa. „Splątanie tworzenia dowolnego stanu dwóch kubitów”. fizyka Wielebny Lett. 80, 2245-2248 (1998).
https: / / doi.org/ 10.1103 / PhysRevLett.80.2245

[89] David P. DiVincenzo, Christopher A. Fuchs, Hideo Mabuchi, John A. Smolin, Ashish Thapliyal i Armin Uhlmann. „Uwikłanie pomocy”. quant-ph/9803033 (1998).
https:///doi.org/10.48550/arXiv.quant-ph/9803033
arXiv: quant-ph / 9803033

[90] Johna A. Smolina, Franka Verstraete i Andreasa Wintera. „Splątanie pomocy i destylacja wielostronna”. Fiz. Rev. A 72, 052317 (2005).
https: / / doi.org/ 10.1103 / PhysRevA.72.052317

[91] Holger F. Hofmann i Shigeki Takeuchi. „Naruszenie lokalnych relacji niepewności jako oznaka splątania”. Fiz. Rev. A 68, 032103 (2003).
https: / / doi.org/ 10.1103 / PhysRevA.68.032103

[92] Otfrieda Gühne. „Charakterystyka splątania poprzez relacje niepewności”. Fiz. Wielebny Lett. 92, 117903 (2004).
https: / / doi.org/ 10.1103 / PhysRevLett.92.117903

[93] Otfried Gühne, Mátyás Mechler, Géza Tóth i Peter Adam. „Kryteria splątania oparte na relacjach lokalnej niepewności są ściśle silniejsze niż obliczalne kryterium krzyżowe”. Fiz. Rev. A 74, 010301 (2006).
https: / / doi.org/ 10.1103 / PhysRevA.74.010301

[94] Giuseppe Vitagliano, Philipp Hyllus, Iñigo L. Egusquiza i Géza Tóth. „Spinowe ściskanie nierówności dla dowolnego spinu”. fizyka Wielebny Lett. 107, 240502 (2011).
https: / / doi.org/ 10.1103 / PhysRevLett.107.240502

[95] AR Edmonds. „Moment pędu w mechanice kwantowej”. Wydawnictwo Uniwersytetu Princeton. (1957).
https: / / doi.org/ 10.1515 / 9781400884186

[96] Geza Tóth. „Wykrywanie splątania w sieciach optycznych atomów bozonowych z pomiarami zbiorczymi”. fizyka Wersja A 69, 052327 (2004).
https: / / doi.org/ 10.1103 / PhysRevA.69.052327

[97] Géza Tóth, Christian Knapp, Otfried Gühne i Hans J. Briegel. „Nierówności ściskania optymalnego spinu wykrywają związane splątanie w modelach spinowych”. fizyka Wielebny Lett. 99, 250405 (2007).
https: / / doi.org/ 10.1103 / PhysRevLett.99.250405

[98] Géza Tóth i Morgan W. Mitchell. „Generowanie makroskopowych stanów singletowych w zespołach atomowych”. Nowy J. Phys. 12, 053007 (2010).
https://doi.org/10.1088/1367-2630/12/5/053007

[99] Géza Tóth. „Wykrywanie splątania wielocząstkowego w sąsiedztwie symetrycznych stanów Dicke’a”. J. Opt. Towarzystwo Jestem. B 24, 275–282 (2007).
https: // doi.org/ 10.1364 / JOSAB.24.000275

[100] Géza Tóth, Tobias Moroder i Otfried Gühne. „Ocena miar splątania dachu wypukłego”. Fiz. Wielebny Lett. 114, 160501 (2015).
https: / / doi.org/ 10.1103 / PhysRevLett.114.160501

[101] Lievena Vandenberghe’a i Stephena Boyda. „Programowanie półokreślone”. Przegląd SIAM 38, 49–95 (1996).
https: / / doi.org/ 10.1137 / 1038003

[102] Geza Tóth. „Splątanie wieloczęściowe i metrologia o wysokiej precyzji”. fizyka Wersja A 85, 022322 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.022322

[103] Philipp Hyllus, Wiesław Laskowski, Roland Krischek, Christian Schwemmer, Witlef Wieczorek, Harald Weinfurter, Luca Pezzé i Augusto Smerzi. „Informacja Fishera i splątanie wielocząstkowe”. fizyka Wersja A 85, 022321 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.022321

[104] Géza Tóth, Tamás Vértesi, Paweł Horodecki i Ryszard Horodecki. „Uruchamianie ukrytej przydatności metrologicznej”. Fiz. Wielebny Lett. 125, 020402 (2020).
https: / / doi.org/ 10.1103 / PhysRevLett.125.020402

[105] AC Doherty, Pablo A. Parrilo i Federico M. Spedalieri. „Rozróżnianie stanów rozłącznych i splątanych”. Fiz. Wielebny Lett. 88, 187904 (2002).
https: / / doi.org/ 10.1103 / PhysRevLett.88.187904

[106] Andrew C. Doherty, Pablo A. Parrilo i Federico M. Spedalieri. „Pełna rodzina kryteriów rozdzielności”. Fiz. Rev. A 69, 022308 (2004).
https: / / doi.org/ 10.1103 / PhysRevA.69.022308

[107] Andrew C. Doherty, Pablo A. Parrilo i Federico M. Spedalieri. „Wykrywanie splątania wielocząstkowego”. Fiz. Rev. A 71, 032333 (2005).
https: / / doi.org/ 10.1103 / PhysRevA.71.032333

[108] Harolda Olliviera i Wojciecha H. Żurka. „Niezgoda kwantowa: miara kwantowości korelacji”. fizyka Wielebny Lett. 88, 017901 (2001).
https: / / doi.org/ 10.1103 / PhysRevLett.88.017901

[109] L. Henderson i V. Vedral. „Korelacje klasyczne, kwantowe i całkowite”. J.Fiz. O: Matematyka. Gen. 34, 6899 (2001).
https://doi.org/10.1088/0305-4470/34/35/315

[110] Anindita Bera, Tamoghna Das, Debasis Sadhukhan, Sudipto Singha Roy, Aditi Sen(De) i Ujjwal Sen. „Kwantowa niezgoda i jej sojusznicy: przegląd ostatniego postępu”. Program Rep. Fiz. 81, 024001 (2017).
https: / / doi.org/ 10.1088 / 1361-6633 / aa872f

[111] Dénes Petz. „Kowariancja i informacja Fishera w mechanice kwantowej”. J.Fiz. O: Matematyka. Gen. 35, 929 (2002).
https://doi.org/10.1088/0305-4470/35/4/305

[112] Paolo Gibilisco, Fumio Hiai i Dénes Petz. „Kowariancja kwantowa, kwantowa informacja Fishera i relacje niepewności”. IEEE Trans. Inf. Teoria 55, 439–443 (2009).
https: / / doi.org/ 10.1109 / TIT.2008.2008142

[113] D. Petz i C. Ghinea. „Wprowadzenie do kwantowej informacji Fishera”. Tom 27, strony 261–281. Świat Naukowy. (2011).
https: / / doi.org/ 10.1142 / 9789814338745_0015

[114] Franka Hansena. „Informacje o skosach skorygowanych metrycznie”. Proc. Natl. Acad. Nauka. USA 105, 9909–9916 (2008).
https: / / doi.org/ 10.1073 / pnas.0803323105

[115] Paolo Gibilisco, Davide Girolami i Frank Hansen. „Ujednolicone podejście do lokalnej niepewności kwantowej i mocy interferometrycznej na podstawie informacji o skośności skorygowanej metrycznie”. Entropia 23, 263 (2021).
https: / / doi.org/ 10.3390 / e23030263

[116] MATLAB. „9.9.0.1524771(r2020b)”. The MathWorks Inc. Natick, Massachusetts (2020).

[117] Aplikacja MOSEK. „Przybornik optymalizacyjny MOSEK dla podręcznika MATLAB. Wersja 9.0”. (2019). adres URL: docs.mosek.com/9.0/toolbox/index.html.
https:///docs.mosek.com/9.0/toolbox/index.html

[118] J. Löfberga. „YALMIP: zestaw narzędzi do modelowania i optymalizacji w MATLABIE”. W materiałach konferencji CACSD. Tajpej, Tajwan (2004).

[119] Géza Tóth. „QUBIT4MATLAB V3.0: Pakiet programów do nauki informacji kwantowej i optyki kwantowej dla MATLAB-a”. Oblicz. Fiz. komuna. 179, 430–437 (2008).
https: / / doi.org/ 10.1016 / j.cpc.2008.03.007

[120] Pakiet QUBIT4MATLAB jest dostępny pod adresem https:///www.mathworks.com/matlabcentral/fileexchange/8433 oraz na osobistej stronie głównej https:///gtoth.eu/qubit4matlab.html.
https:///www.mathworks.com/matlabcentral/fileexchange/8433

Cytowany przez

[1] Laurent Lafleche, „Kwantowy transport optymalny i słabe topologie”, arXiv: 2306.12944, (2023).

Powyższe cytaty pochodzą z Reklamy SAO / NASA (ostatnia aktualizacja pomyślnie 2023-10-16 14:47:44). Lista może być niekompletna, ponieważ nie wszyscy wydawcy podają odpowiednie i pełne dane cytowania.

Nie można pobrać Przywołane przez Crossref dane podczas ostatniej próby 2023-10-16 14:47:42: Nie można pobrać cytowanych danych dla 10.22331 / q-2023-10-16-1143 z Crossref. Jest to normalne, jeśli DOI zostało niedawno zarejestrowane.

Niniejszy artykuł opublikowano w Quantum pod Creative Commons Uznanie autorstwa 4.0 Międzynarodowe (CC BY 4.0) licencja. Prawa autorskie należą do pierwotnych właścicieli praw autorskich, takich jak autorzy lub ich instytucje.

Dystrybucja treści i PR oparta na SEO. Uzyskaj wzmocnienie już dziś.
PlatoData.Network Pionowe generatywne AI. Wzmocnij się. Dostęp tutaj.
PlatoAiStream. Inteligencja Web3. Wiedza wzmocniona. Dostęp tutaj.
PlatonESG. Węgiel Czysta technologia, Energia, Środowisko, Słoneczny, Gospodarowanie odpadami. Dostęp tutaj.
Platon Zdrowie. Inteligencja w zakresie biotechnologii i badań klinicznych. Dostęp tutaj.
Źródło: https://quantum-journal.org/papers/q-2023-10-16-1143/

Znak czasu: 16 października 2023 r.

Znak czasu: Październik 6, 2022

Opublikowane ponownie przez Plato

Adaptacyjny filtr pomiarowy: wydajna strategia optymalnej estymacji kwantowych łańcuchów Markowa

Dynamika splątania w symetrycznych obwodach hybrydowego automatu kwantowego U(1).

Kody kwantowe LDPC dostosowane do odchylenia

Kiedy przybywa cząsteczka?

Ograniczenia podejścia macierzowego Macaulaya do wykorzystania algorytmu HHL do rozwiązywania wielowymiarowych układów wielomianowych

Informacja kwantowa z górnymi kwarkami w QCD

Algorytm kwantowego przekazywania wiadomości dla optymalnego i wydajnego dekodowania

Minimalny koszt komunikacji przy symulowaniu splątanych kubitów

Kwantowa manipulacja dwupoziomowym systemem mechanicznym

Przygotowanie stanu termicznego poprzez obietnice zaokrągleń

Kwantowe uczenie wariacyjne dla kodów korekcji błędów kwantowych

O nas

Wyszukiwanie pionowe i AI

Platforma

Pozostań w kontakcie

Konto