Ciągła majoryzacja w kwantowej przestrzeni fazowej

Ciągła majoryzacja w kwantowej przestrzeni fazowej

Znacznik czasu: 24 maja 2023 r. 7:39
Węzeł źródłowy: 2674950

Zachariasz Van Herstraeten1,2, Michaela G. Jabboura1,3,4i Nicolas J. Cerf1

1Centrum Informacji i Komunikacji Kwantowej, École polytechnique de Bruxelles, CP 165/59, Université libre de Bruxelles, 1050 Bruksela, Belgia
2Wyant College of Optical Sciences, University of Arizona, 1630 E. University Blvd., Tucson, AZ 85721, USA
3DAMTP, Centrum Nauk Matematycznych, Uniwersytet Cambridge, Cambridge CB3 0WA, Wielka Brytania
4Wydział Fizyki, Duński Uniwersytet Techniczny, 2800 Kongens Lyngby, Dania

Czy ten artykuł jest interesujący czy chcesz dyskutować? Napisz lub zostaw komentarz do SciRate.

Abstrakcyjny

Badamy rolę teorii majoryzacji w kwantowej przestrzeni fazowej. W tym celu ograniczamy się do stanów kwantowych z dodatnimi funkcjami Wignera i pokazujemy, że ciągła wersja teorii majoryzacji zapewnia eleganckie i bardzo naturalne podejście do badania informacyjno-teoretycznych właściwości funkcji Wignera w przestrzeni fazowej. Po zidentyfikowaniu wszystkich czystych stanów Gaussa jako równoważnych w dokładnym sensie ciągłej majoryzacji, co można zrozumieć w świetle twierdzenia Hudsona, przypuszczamy podstawową relację majoryzacji: każda dodatnia funkcja Wignera jest majoryzowana przez funkcję Wignera czystego stanu Gaussa (zwłaszcza , bozonowy stan próżni lub stan podstawowy oscylatora harmonicznego). W konsekwencji każda wklęsła funkcja Schura funkcji Wignera jest dolna ograniczona przez wartość, jaką przyjmuje dla stanu próżni. Oznacza to z kolei, że entropia Wignera jest dolna granica jej wartości dla stanu próżni, podczas gdy sytuacja odwrotna nie jest w szczególności prawdą. Naszym głównym wynikiem jest zatem udowodnienie tej podstawowej relacji majoryzacji dla odpowiedniego podzbioru dodatnich stanów kwantowych Wignera, które są mieszaninami trzech najniższych stanów własnych oscylatora harmonicznego. Poza tym przypuszczenie to jest poparte dowodami liczbowymi. Na koniec omówimy niektóre implikacje tego przypuszczenia w kontekście entropicznych relacji niepewności w przestrzeni fazowej.

Popularne podsumowanie

Zasada nieoznaczoności jest jednym z najbardziej fascynujących zjawisk w fizyce kwantowej. Chociaż może się wydawać naturalne, że pary mierzalnych wielkości, takich jak położenie i pęd cząstki, można dokładnie przewidzieć jednocześnie, fizyka kwantowa w rzeczywistości zabrania tego w przypadku obiektów niekomutujących. Heisenberg i Kennard doprecyzowali to, wykorzystując wariancję dowolnej mierzalnej wielkości, aby uchwycić jej niepewność. Wiele lat później zasada nieoznaczoności Heisenberga została przeformułowana, zwracając się do entropii jako właściwego środka do ilościowego określania niepewności. Tutaj wprowadzamy jeszcze silniejszy paradygmat informacyjno-teoretyczny do zrozumienia niepewności zmiennych kwantowych w przestrzeni fazowej, a mianowicie teorię majoryzacji.

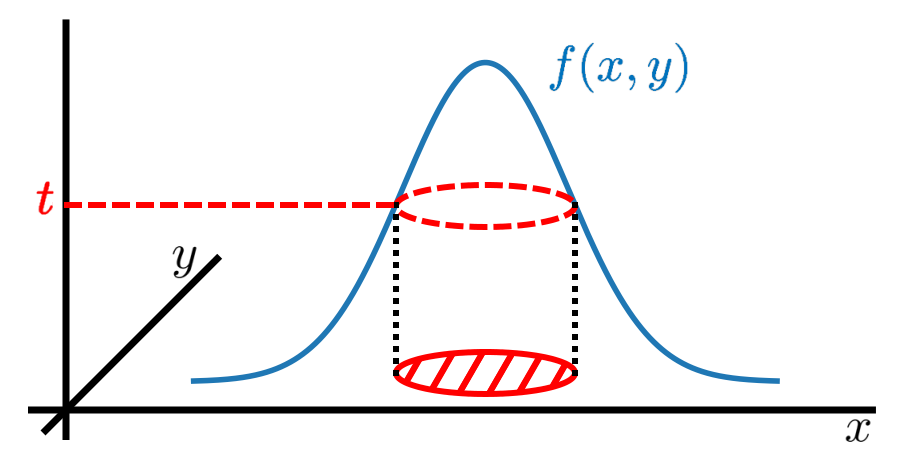
Ta teoria matematyczna została opracowana ponad sto lat temu i była wykorzystywana w wielu dziedzinach nauki, od statystyki po fizykę. Co ciekawe, została zastosowana w fizyce kwantowej dopiero stosunkowo niedawno, gdzie wykazano, że jest to potężne podejście do badania splątania kwantowego. Jako taka, nigdy nie została wykorzystana do scharakteryzowania ciągłych gęstości opisujących zmienne kwantowe w przestrzeni fazowej, to znaczy funkcji Wignera. Pokazujemy, że ciągła majoryzacja jest do tego odpowiednim narzędziem. Główny wątek naszego artykułu dotyczy stwierdzenia, że ​​funkcja Wignera stanu próżni modu bozonowego (tj. stanu podstawowego oscylatora harmonicznego) jest ciągłą majoryzacją każdej innej funkcji Wignera, czyniąc ją mniej niepewną w sensie majoryzacji .

Chociaż ujawniamy i omawiamy nasze wyniki w kontekście optyki kwantowej, przenoszą się one do dowolnej pary kanonicznej i dlatego powinny mieć implikacje w różnych obszarach fizyki.

► Dane BibTeX

► Referencje

[1] G. H. Hardy, J. E. Littlewood i G. Pólya, „Nierówności”. Cambridge University Press, 1934.
https: / / doi.org/ 10.2307 / 3605504

[2] A. W. Marshall, I. Olkin i BC Arnold, „Nierówności: teoria majoryzacji i jej zastosowania”, tom. 143. Springer, wyd. drugie, 2011.
https:/​/​doi.org/​10.1007/​978-0-387-68276-1

[3] T. Ando, ​​„Majoryzacja, podwójnie stochastyczne macierze i porównanie wartości własnych”, Linear Algebra Appl. 118, 163–248 (1989).
https:/​/​doi.org/​10.1016/​0024-3795(89)90580-6

[4] K. Mosler, „Majorization in Economic Disparity Measures”, Linear Algebra and his Applications 199, 91–114 (1994).
https:/​/​doi.org/​10.1016/​0024-3795(94)90343-3

[5] T. van Erven i P. Harremoës, „Rényi dywergencja i majoryzacja”, w 2010 r. Międzynarodowe sympozjum IEEE na temat teorii informacji, s. 1335–1339, IEEE. 2010.
https: / / doi.org/ 10.1109 / ISIT.2010.5513784

[6] M. A. Alhejji i G. Smith, „A Tight Uniform Continuity Bound for Equivocation”, w 2020 r. Międzynarodowe sympozjum IEEE na temat teorii informacji (ISIT), s. 2270–2274. 2020.
https://​/​doi.org/​10.1109/​ISIT44484.2020.9174350

[7] MG Jabbour i N. Datta, „A Tight Uniform Continuity Bound for the Arimoto-Rényi Conditional Entropy and his Extension to Classical-Quantum States”, „IEEE Transactions on Information Theory 68, 2169–2181 (2022).
https: / / doi.org/ 10.1109 / TIT.2022.3142812

[8] A. Horn, „Podwójnie stochastyczne macierze i przekątna macierzy rotacyjnej”, American Journal of Mathematics 76, 620–630 (1954).
https: / / doi.org/ 10.2307 / 2372705

[9] MA Nielsen, „Warunki dla klasy transformacji splątania”, „Physical Review Letters” 83, 436 (1999).
https: / / doi.org/ 10.1103 / PhysRevLett.83.436

[10] MA Nielsen i G. Vidal, „Majorization and the interconversion of bipartite States”, Quantum Information and Computation 1, 76–93 (2001).
https: / / doi.org/ 10.26421 / QIC1.1-5

[11] M. A. Nielsen i J. Kempe, „Oddzielne państwa są bardziej zaburzone globalnie niż lokalnie”, Physical Review Letters 86, 5184–5187 (2001).
https: / / doi.org/ 10.1103 / PhysRevLett.86.5184

[12] T. Hiroshima, „Kryterium majoryzacji destylacji dwustronnego stanu kwantowego”, Physical Review Letters 91, 057902 (2003).
https: / / doi.org/ 10.1103 / PhysRevLett.91.057902

[13] Z. Puchała, Ł. Rudnicki i K. Życzkowski, „Majorization entropic niepewność relacji”, Journal of Physics A: Mathematical and Theoretical 46, 272002 (2013).
https:/​/​doi.org/​10.1088/​1751-8113/​46/​27/​272002

[14] L. Rudnicki, Z. Puchała i K. Życzkowski, „Relacje niepewności entropicznej silnej majoryzacji”, Physical Review A 89, 052115 (2014).
https: / / doi.org/ 10.1103 / PhysRevA.89.052115

[15] L. Rudnicki, ``Podejście majoryzacyjne do relacji niepewności entropicznej dla gruboziarnistych obserwowalnych'', Physical Review A 91, 032123 (2015).
https: / / doi.org/ 10.1103 / PhysRevA.91.032123

[16] F. Brandão, M. Horodecki, N. Ng, J. Oppenheim i S. Wehner, „Drugie prawa termodynamiki kwantowej”, Proceedings of the National Academy of Sciences 112, 3275–3279 (2015).
https: / / doi.org/ 10.1073 / pnas.1411728112

[17] R. García-Patrón, C. Navarrete-Benlloch, S. Lloyd, J. H. Shapiro i N. J. Cerf, „Majorization Theory Approach to the Gaussian Channel Minimum Entropy Conjecture”, Physical Review Letters 108, 110505 (2012).
https: / / doi.org/ 10.1103 / PhysRevLett.108.110505

[18] C. N. Gagatsos, O. Oreshkov i N. J. Cerf, „Relacje majoryzacji i generowanie splątania w rozdzielaczu wiązki”, Physical Review A 87, 042307 (2013).
https: / / doi.org/ 10.1103 / PhysRevA.87.042307

[19] G. De Palma, D. Trevisan i V. Giovannetti, „Stany pasywne optymalizują dane wyjściowe bozonowych kanałów kwantowych Gaussa”, IEEE Transactions on Information Theory 62, 2895–2906 (2016).
https: / / doi.org/ 10.1109 / TIT.2016.2547426

[20] M. G. Jabbour, R. García-Patrón i N. J. Cerf, „Majorizationkonservation of Gaussian bosonic Channels”, New Journal of Physics 18, 073047 (2016).
https:/​/​doi.org/​10.1088/​1367-2630/​18/​7/​073047

[21] M. G. Jabbour i N. J. Cerf, „Fock majorization in bosonic Quantum Channels with a Passive Environment”, Journal of Physics A: Mathematical and Theoretical 52, 105302 (2019).
https:/​/​doi.org/​10.1088/​1751-8121/​aaf0d2

[22] U. Leonhardt, „Podstawowa optyka kwantowa: od pomiarów kwantowych do czarnych dziur”. Cambridge University Press, 2010.
https: / / doi.org/ 10.1017 / CBO9780511806117

[23] A. Hertz, M. G. Jabbour i N. J. Cerf, „Relacje niepewności entropii i mocy: w kierunku ścisłej nierówności dla wszystkich czystych stanów Gaussa”, Journal of Physics A: Mathematical and Theoretical 50, 385301 (2017).
https: / / doi.org/ 10.1088 / 1751-8121 / aa852f

[24] A. Hertz i N. J. Cerf, „Relacje niepewności entropicznej ciągłej zmiennej”, Journal of Physics A: Mathematical and Theoretical 52, 173001 (2019).
https:/​/​doi.org/​10.1088/​1751-8121/​ab03f3

[25] C. Weedbrook, S. Pirandola, R. García-Patrón, N. J. Cerf, TC Ralph, J. H. Shapiro i S. Lloyd, „Gaussian quantum Information”, Review of Modern Physics 84, 621–669 (2012).
https: / / doi.org/ 10.1103 / RevModPhys.84.621

[26] Z. Van Herstraeten i N. J. Cerf, „Quantum Wigner entropy”, Physical Review A 104, 042211 (2021).
https: / / doi.org/ 10.1103 / PhysRevA.104.042211

[27] F. J. Narcowich, ``Rozkłady typu $hbar$-pozytywnego i zastosowania'' Journal of matematycznej fizyki 30, 2565–2573 (1989).
https: / / doi.org/ 10.1063 / 1.528537

[28] T. Bröcker i R. Werner, „Stany mieszane z dodatnimi funkcjami Wignera”, Journal of matematyczna fizyka 36, ​​62–75 (1995).
https: / / doi.org/ 10.1063 / 1.531326

[29] RL Hudson, „Kiedy gęstość quasi-prawdopodobieństwa Wignera jest nieujemna?”, Reports on Mathematical Physics 6, 249–252 (1974).
https:/​/​doi.org/​10.1016/​0034-4877(74)90007-X

[30] F. Soto i P. Claverie, „Kiedy funkcja Wignera w systemach wielowymiarowych jest nieujemna?”, Journal of Mathematical Physics 24, 97–100 (1983).
https: / / doi.org/ 10.1063 / 1.525607

[31] F. J. Narcowich i R. O'Connell, „Warunki konieczne i wystarczające, aby funkcja przestrzeni fazowej była rozkładem Wignera”, Physical Review A 34, 1 (1986).
https: / / doi.org/ 10.1103 / PhysRevA.34.1

[32] A. Mandilara, E. Karpov i N. J. Cerf, „Rozszerzanie twierdzenia Hudsona na mieszane stany kwantowe”, Physical Review A 79, 062302 (2009).
https: / / doi.org/ 10.1103 / PhysRevA.79.062302

[33] A. Mandilara, E. Karpov i N. Cerf, „Granice Gaussa dla kwantowych stanów mieszanych z dodatnią funkcją Wignera”, w Journal of Physics: Conference Series, tom. 254, s. 012011, Wydawnictwo IOP. 2010.
https:/​/​doi.org/​10.1088/​1742-6596/​254/​1/​012011

[34] L. Wang i M. Madiman, „Beyond the Entropy Power Inequality, via Rearrangements”, IEEE Transactions on Information Theory 60, 5116–5137 (2014).
https: / / doi.org/ 10.1109 / TIT.2014.2338852

[35] G. H. Hardy, JE Littlewood i G. Pólya, „Niektóre proste nierówności spełniane przez funkcje wypukłe”, Messenger of Mathematics 58, 145–152 (1929).

[36] H. Joe, „Porządek zależności dla dystrybucji k-krotek, z zastosowaniami do gier lotto”, Canadian Journal of Statistics 15, 227–238 (1987).
https: / / doi.org/ 10.2307 / 3314913

[37] I. Schur, „Uber eine Klasse von Mittelbildungen mit Anwendungen die Determinanten”, Sitzungsberichte der Berliner Mathematischen Gesellschaft 22, 416–427 (1923).

[38] A. W. Roberts i D. E. Varberg, „Funkcje wypukłe”. Prasa akademicka Nowy Jork, 1973.
https:/​/​doi.org/​10.1016/​B978-0-444-89597-4.50013-5

[39] A. Rényi, „O miarach entropii i informacji” w: Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, tom 1: Contributions to the Theory of Statistics, tom. 4, s. 547–562, University of California Press. 1961.

[40] Y. He, AB Hamza i H. Krim, „Uogólniona miara rozbieżności dla solidnej rejestracji obrazu”, IEEE Transactions on Signal Processing 51, 1211–1220 (2003).
https://​/​doi.org/​10.1109/​TSP.2003.810305

[41] J. V. Ryff, „Orbity $L^1$ -funkcje w warunkach podwójnie stochastycznych transformacji”, Transactions of the American Mathematical Society 117, 92–100 (1965).
https: / / doi.org/ 10.2307 / 1994198

[42] F. Bahrami, SM Manjegani i S. Moein, „Semi-doubly Stochastic Operators and Majorization of Całkowalne funkcje”, Bulletin of the Malaysian Mathematical Sciences Society 44, 693–703 (2021).
https:/​/​doi.org/​10.1007/​s40840-020-00971-2

[43] S. M. Manjegani i S. Moein, „Majorization and semidoubly stochastic operators on $ L^{1}(X)$”, Journal of Inequalities and Applications 2023, 1–20 (2023).
https: / / doi.org/ 10.1186 / s13660-023-02935-z

[44] I. Białynicki-Birula i J. Mycielski, „Relacje niepewności dla entropii informacji w mechanice falowej”, Communications in Mathematical Physics 44, 129–132 (1975).
https: / / doi.org/ 10.1007 / BF01608825

[45] A. Wehrl, „Ogólne właściwości entropii”, Recenzje Modern Physics 50, 221 (1978).
https: / / doi.org/ 10.1103 / RevModPhys.50.221

[46] E. H. Lieb, „Dowód hipotezy Wehrla o entropii”, w: Inequalities, s. 359–365. Springer, 2002.
https:/​/​doi.org/​10.1007/​978-3-642-55925-9_30

[47] E. H. Lieb i J. P. Solovej, „Dowód hipotezy entropii dla spójnych stanów spinowych Blocha i jego uogólnień”, Acta Mathematica 212, 379 (2014).
https:/​/​doi.org/​10.1007/​s11511-014-0113-6

[48] J. R. Johansson, PD Nation i F. Nori, „QuTiP: platforma Pythona o otwartym kodzie źródłowym dla dynamiki otwartych systemów kwantowych”, Computer Physics Communications 183, 1760–1772 (2012).
https: / / doi.org/ 10.1016 / j.cpc.2012.02.021

[49] K. Życzkowski, P. Horodecki, A. Sanpera i M. Lewenstein, „Objętość zbioru stanów separowalnych”, Physical Review A 58, 883 (1998).
https: / / doi.org/ 10.1103 / PhysRevA.58.883

Cytowany przez

[1] Nuno Costa Dias i João Nuno Prata, „Na podstawie niedawnych przypuszczeń Z. Van Herstraetena i N.J. Cerfa na temat kwantowej entropii Wignera”, arXiv: 2303.10531, (2023).

[2] Zacharie Van Herstraeten i Nicolas J. Cerf, „Quantum Wigner entropy”, Przegląd fizyczny A 104 4, 042211 (2021).

[3] Martin Gärttner, Tobias Haas i Johannes Noll, „Wykrywanie ciągłego splątania zmiennych w przestrzeni fazowej za pomocą rozkładu $Q$”, arXiv: 2211.17165, (2022).

Powyższe cytaty pochodzą z Reklamy SAO / NASA (ostatnia aktualizacja pomyślnie 2023-05-24 23:55:18). Lista może być niekompletna, ponieważ nie wszyscy wydawcy podają odpowiednie i pełne dane cytowania.

On Serwis cytowany przez Crossref nie znaleziono danych na temat cytowania prac (ostatnia próba 2023-05-24 23:55:17).

Niniejszy artykuł opublikowano w Quantum pod Creative Commons Uznanie autorstwa 4.0 Międzynarodowe (CC BY 4.0) licencja. Prawa autorskie należą do pierwotnych właścicieli praw autorskich, takich jak autorzy lub ich instytucje.

Znak czasu:

Więcej z Dziennik kwantowy