1量子情報通信センター、ブリュッセル工科大学、CP 165/59、ブリュッセル自由大学、1050 ブリュッセル、ベルギー
2アリゾナ大学ワイアント光学科学大学、1630 E. University Blvd.、ツーソン、アリゾナ州 85721、米国
3DAMTP、数理科学センター、ケンブリッジ大学、ケンブリッジ CB3 0WA、英国
4デンマーク工科大学物理学科、2800 Kongens Lyngby、デンマーク
この論文を興味深いと思うか、議論したいですか? SciRateを引用するかコメントを残す.
抽象
量子位相空間におけるメジャー化理論の役割を探ります。この目的のために、我々は、正のウィグナー関数を持つ量子状態に限定し、マジョリゼーション理論の連続バージョンが、位相空間におけるウィグナー関数の情報理論的特性を探索するための洗練された非常に自然なアプローチを提供することを示します。ハドソンの定理に照らして理解できる、連続メジャー化の正確な意味ですべてのガウス純粋状態が等価であると特定した後、基本的なメジャー化関係を推測します。正のウィグナー関数はすべて、ガウス純粋状態 (特に、特に) のウィグナー関数によってメジャー化されます。 、ボソン真空状態または調和振動子の基底状態)。結果として、ウィグナー関数のシュール凹関数は、真空状態の値によって下限が制限されます。これは、ウィグナー エントロピーの下限が真空状態の値によって制限されることを意味しますが、その逆は特に当てはまりません。我々の主な結果は、調和振動子の 3 つの最低固有状態の混合であるウィグナー正の量子状態の関連サブセットについて、この基本的なメジャー化関係を証明することです。さらに、この推測は数値的な証拠によっても裏付けられています。最後に、位相空間におけるエントロピー不確実性関係の文脈におけるこの予想のいくつかの意味について議論します。
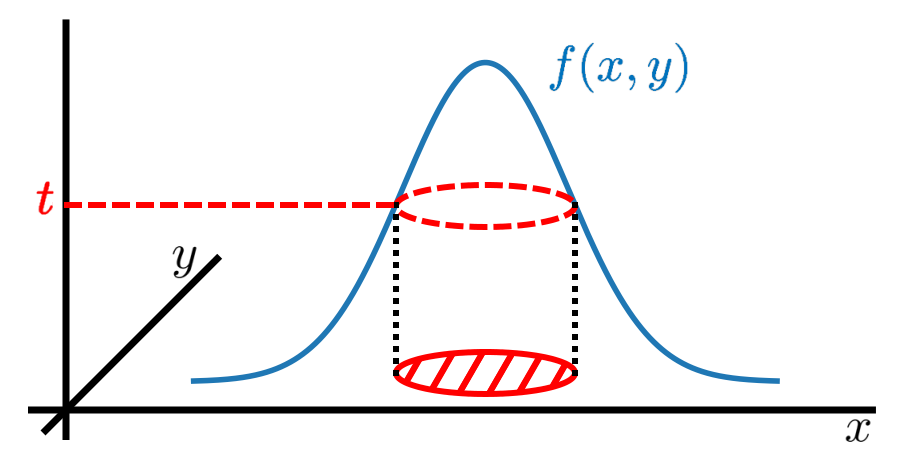
人気の要約
この数学理論は XNUMX 世紀以上前に開発され、統計から物理学に至るまで、数多くの科学分野で使用されてきました。 注目すべきことに、量子物理学に適用されたのは比較的最近になってからであり、量子もつれを探索するための強力なアプローチであることが示されています。 そのため、位相空間内の量子変数、つまりウィグナー関数を記述する連続密度を特徴付けるために利用されたことはありません。 我々は、継続的メジャー化がこれに適したツールであることを示します。 私たちの論文の主な目的は、ボソンモードの真空状態(つまり、調和振動子の基底状態)のウィグナー関数が他のウィグナー関数を連続多数化し、多数派化という意味での不確実性がより低くなるという主張に関するものです。 。
私たちは量子光学の文脈で結果を公開し議論しますが、それらはあらゆる正準ペアに引き継がれるため、物理学のさまざまな分野に影響を与えるはずです。
►BibTeXデータ
►参照
【1] G. H. ハーディ、J. E. リトルウッド、G. ポリャ、「不平等」。ケンブリッジ大学出版局、1934 年。
https:/ / doi.org/ 10.2307 / 3605504
【2] A. W. マーシャル、I. オルキン、および B. C. アーノルド、「不等式: メジャー化の理論とその応用」、第 143 巻。 2011. Springer、第 XNUMX 版、XNUMX 年。
https://doi.org/10.1007/978-0-387-68276-1
【3] T. Ando、「多数化、二重確率行列、および固有値の比較」、Linear Algebra Appl. 118、163–248 (1989)。
https://doi.org/10.1016/0024-3795(89)90580-6
【4] K. Mosler、「経済格差対策における重要性」、Linear Algebra and its Applications 199、91–114 (1994)。
https://doi.org/10.1016/0024-3795(94)90343-3
【5] T. van Erven および P. Harremoës、「Rényi divergence and Majorization」、2010 年の IEEE 情報理論国際シンポジウム、1335 ~ 1339 ページ、IEEE。 2010年。
https:/ / doi.org/ 10.1109 / ISIT.2010.5513784
【6] M. A. Alhejji および G. Smith、「A Tight Unique Continuity Bound for Equivocation」、2020 IEEE International Symposium on Information Theory (ISIT)、2270–2274 ページ。 2020年。
https:/ / doi.org/ 10.1109 / ISIT44484.2020.9174350
【7] M. G. Jabbour および N. Datta、「Arimoto-Rényi 条件付きエントロピーとその古典量子状態への拡張に限定されたタイトな均一連続性」、IEEE 情報理論トランザクション 68、2169–2181 (2022)。
https:/ / doi.org/ 10.1109 / TIT.2022.3142812
【8] A. Horn、「二重確率行列と回転行列の対角線」、American Journal of Mathematics 76、620–630 (1954)。
https:/ / doi.org/ 10.2307 / 2372705
【9] M. A. Nielsen、「Conditions for a Class of Entanglement Transformations」、Physical Review Letters 83、436 (1999)。
https:/ / doi.org/ 10.1103 / PhysRevLett.83.436
【10] M. A. ニールセンおよび G. ヴィダル、「二部構成状態の多数化と相互変換」、量子情報と計算 1、76–93 (2001)。
https:/ / doi.org/ 10.26421 / QIC1.1-5
【11] M. A. ニールセンと J. ケンペ、「分離可能な国家は局地的よりも世界的により無秩序である」、Physical Review Letters 86、5184–5187 (2001)。
https:/ / doi.org/ 10.1103 / PhysRevLett.86.5184
【12] T. 広島、「二部量子状態の蒸留性に関する主要化基準」、Physical Review Letters 91、057902 (2003)。
https:/ / doi.org/ 10.1103 / PhysRevLett.91.057902
【13] Z. プチャワ、Ł. Rudnicki、K. Życzkowski、「Majorization entropic不確定性関係」、Journal of Physics A: Mathematical and Theoretical 46、272002 (2013)。
https://doi.org/10.1088/1751-8113/46/27/272002
【14] L. Rudnicki、Z. Puchała、および K. Życzkowski、「強いメジャー化エントロピーの不確実性関係」、Physical Review A 89、052115 (2014)。
https:/ / doi.org/ 10.1103 / PhysRevA.89.052115
【15] L. Rudnicki、「粗粒観測値のエントロピー不確実性関係への多数化アプローチ」、Physical Review A 91、032123 (2015)。
https:/ / doi.org/ 10.1103 / PhysRevA.91.032123
【16] F. Brandão、M. Horodecki、N. Ng、J. Oppenheim、および S. Wehner、「量子熱力学の第 112 法則」、米国科学アカデミー紀要 3275、3279–2015 (XNUMX)。
https:/ / doi.org/ 10.1073 / pnas.1411728112
【17] R. García-Patron、C. Navarrete-Benlloch、S. Lloyd、J. H. Shapiro、および N. J. Cerf、「ガウス チャネル最小エントロピー予想への多数決理論アプローチ」、Physical Review Letters 108、110505 (2012)。
https:/ / doi.org/ 10.1103 / PhysRevLett.108.110505
【18] C. N. Gagatsos、O. Oreshkov、および N. J. Cerf、「ビーム スプリッターにおける多数決関係ともつれの生成」、Physical Review A 87、042307 (2013)。
https:/ / doi.org/ 10.1103 / PhysRevA.87.042307
【19] G. De Palma、D. Trevisan、および V. Giovannetti、「パッシブ ステートはボソン ガウス量子チャネルの出力を最適化する」、IEEE Transactions on Information Theory 62、2895–2906 (2016)。
https:/ / doi.org/ 10.1109 / TIT.2016.2547426
【20] M. G. Jabbour、R. García-Patrón、および N. J. Cerf、「ガウス ボソン チャネルの主要化保存」、New Journal of Physics 18、073047 (2016)。
https://doi.org/10.1088/1367-2630/18/7/073047
【21] M. G. Jabbour および N. J. Cerf、「受動的環境を伴うボソン量子チャネルのフォックメジャー化」、Journal of Physics A: Mathematical and Theoretical 52、105302 (2019)。
https://doi.org/10.1088/1751-8121/aaf0d2
【22] U. Leonhardt、「本質的な量子光学: 量子測定からブラック ホールまで」。ケンブリッジ大学出版局、2010 年。
https:/ / doi.org/ 10.1017 / CBO9780511806117
【23] A. Hertz、M. G. Jabbour、および N. J. Cerf、「エントロピーとパワーの不確実性の関係: すべてのガウス純粋状態に対する厳しい不平等に向けて」、Journal of Physics A: Mathematical and Theoretical 50、385301 (2017)。
https:/ / doi.org/ 10.1088 / 1751-8121 / aa852f
【24] A. Hertz および N. J. Cerf、「連続変数エントロピーの不確実性関係」、Journal of Physics A: Mathematical and Theoretical 52、173001 (2019)。
https://doi.org/10.1088/1751-8121/ab03f3
【25] C. Weedbrook、S. Pirandola、R. García-Patrón、N. J. Cerf、T. C. Ralph、J. H. Shapiro、および S. Lloyd、「ガウス量子情報」、Review of Modern Physics 84、621–669 (2012)。
https:/ / doi.org/ 10.1103 / RevModPhys.84.621
【26] Z. Van Herstraeten および N. J. Cerf、「Quantum Wigner entropy」、Physical Review A 104、042211 (2021)。
https:/ / doi.org/ 10.1103 / PhysRevA.104.042211
【27] F. J. Narcowich、「$hbar$ 陽性タイプの分布と応用」、Journal of mathphysics 30、2565–2573 (1989)。
https:/ / doi.org/ 10.1063 / 1.528537
【28] T. Bröcker および R. Werner、「正のウィグナー関数を持つ混合状態」、Journal of mathphysics 36、62–75 (1995)。
https:/ / doi.org/ 10.1063 / 1.531326
【29] R. L. Hudson、「ウィグナー準確率密度が非負になるのはいつですか?」、Reports on Mathematical Physics 6、249–252 (1974)。
https://doi.org/10.1016/0034-4877(74)90007-X
【30] F. Soto および P. Claverie、「多次元システムのウィグナー関数が非負になるのはいつか?」、Journal of Mathematical Physics 24、97–100 (1983)。
https:/ / doi.org/ 10.1063 / 1.525607
【31] F. J. Narcowich および R. O’Connell、「位相空間関数がウィグナー分布であるための必要十分条件」、Physical Review A 34、1 (1986)。
https:/ / doi.org/ 10.1103 / PhysRevA.34.1
【32] A. Mandilara、E. Karpov、および N. J. Cerf、「ハドソンの定理を混合量子状態に拡張する」、Physical Review A 79、062302 (2009)。
https:/ / doi.org/ 10.1103 / PhysRevA.79.062302
【33] A. Mandilara、E. Karpov、および N. Cerf、「正のウィグナー関数を持つ量子混合状態のガウス境界」、Journal of Physics: Conference Series、vol. 254、p. 012011、IOP出版。 2010年。
https://doi.org/10.1088/1742-6596/254/1/012011
【34] L. Wang および M. Madiman、「再配置によるエントロピー パワーの不平等を超えて」、IEEE Transactions on Information Theory 60、5116–5137 (2014)。
https:/ / doi.org/ 10.1109 / TIT.2014.2338852
【35] G. H. Hardy、J. E. Littlewood、および G. Pólya、「凸関数によって満足されるいくつかの単純な不等式」、Messenger of Mathematics 58、145–152 (1929)。
【36] H. Joe、「ロト ゲームへの応用を伴う、k タプルの配布のための依存性の順序付け」、Canadian Journal of Statistics 15、227–238 (1987)。
https:/ / doi.org/ 10.2307 / 3314913
【37] I. Schur、「Uber eine Klasse von Mittelbildungen mit Anwendungen die Determinanten」、Sitzungsberichte der Berliner Mathematischen Gesellschaft 22、416–427 (1923)。
【38] A. W. Roberts と D. E. Varberg、「凸関数」。アカデミックプレス、ニューヨーク、1973年。
https://doi.org/10.1016/B978-0-444-89597-4.50013-5
【39] A. Rényi、「エントロピーと情報の測定について」、数学的統計と確率に関する第 1 回バークレー シンポジウム議事録、第 4 巻: 統計理論への貢献、第 547 巻。 562、1961–XNUMXページ、カリフォルニア大学出版局。 XNUMX年。
【40] Y. He、A. B. Hamza、および H. Krim、「堅牢な画像レジストレーションのための一般化された発散測定」、IEEE Transactions on Signal Processing 51、1211–1220 (2003)。
https:/ / doi.org/ 10.1109/ TSP.2003.810305
【41] J. V. Ryff、「二重確率変換下の $L^1$ 関数の軌道」、Transactions of the American Mathematical Society 117、92–100 (1965)。
https:/ / doi.org/ 10.2307 / 1994198
【42] F. Bahrami、S. M. Manjegani、および S. Moein、「準二重確率演算子と可積分関数のメジャー化」、マレーシア数理科学協会紀要 44、693–703 (2021)。
https://doi.org/10.1007/s40840-020-00971-2
【43] S. M. Manjegani および S. Moein、「$ L^{1}(X)$ の多数決および半二重確率演算子」、Journal of Inequalities and Applications 2023、1–20 (2023)。
https:/ / doi.org/ 10.1186 / s13660-023-02935-z
【44] I. Białynicki-Birula および J. Mycielski、「波力学における情報エントロピーの不確実性関係」、Communications in Mathematical Physics 44、129–132 (1975)。
https:/ / doi.org/ 10.1007 / BF01608825
【45] A. Wehrl、「エントロピーの一般特性」、Review of Modern Physics 50、221 (1978)。
https:/ / doi.org/ 10.1103 / RevModPhys.50.221
【46] E. H. Lieb、「Wehrl のエントロピー予想の証明」、『不等式』、359 ~ 365 ページ。スプリンガー、2002 年。
https://doi.org/10.1007/978-3-642-55925-9_30
【47] E. H. Lieb および J. P. Solovej、「ブロッホ コヒーレント スピン状態のエントロピー予想とその一般化の証明」、Acta Mathematica 212、379 (2014)。
https://doi.org/10.1007/s11511-014-0113-6
【48] J. R. Johansson、P. D. Nation、および F. Ori、「QuTiP: オープン量子システムのダイナミクスのためのオープンソース Python フレームワーク」、Computer Physics Communications 183、1760–1772 (2012)。
https:/ / doi.org/ 10.1016 / j.cpc.2012.02.021
【49] K. Życzkowski、P. Horodecki、A. Sanpera、および M. Lewenstein、「分離可能な状態のセットのボリューム」、Physical Review A 58、883 (1998)。
https:/ / doi.org/ 10.1103 / PhysRevA.58.883
によって引用
[1] Nuno Costa Dias と João Nuno Prata、「量子ウィグナーエントロピーに関する Z. Van Herstraeten と N.J. Cerf による最近の予想について」、 arXiv:2303.10531, (2023).
[2] ザカリー・ヴァン・ヘルシュトレーテンとニコラス・J・サーフ、「量子ウィグナー・エントロピー」、 フィジカルレビューA 104 4、042211(2021).
[3] Martin Gärttner、Tobias Haas、Johannes Noll、「$Q$ 分布を使用した位相空間における連続変数もつれの検出」、 arXiv:2211.17165, (2022).
上記の引用は SAO / NASA ADS (最後に正常に更新された2023-05-24 23:55:18)。 すべての出版社が適切で完全な引用データを提供するわけではないため、リストは不完全な場合があります。
On Crossref の引用サービス 作品の引用に関するデータは見つかりませんでした(最後の試行2023-05-24 23:55:17)。
この論文は、 Creative Commons Attribution 4.0 International(CC BY 4.0) ライセンス。 著作権は、著者やその機関などの元の著作権者にあります。
- SEO を活用したコンテンツと PR 配信。 今日増幅されます。
- プラトアイストリーム。 Web3 データ インテリジェンス。 知識増幅。 こちらからアクセスしてください。
- 未来を鋳造する w エイドリエン・アシュリー。 こちらからアクセスしてください。
- PREIPO® を使用して PRE-IPO 企業の株式を売買します。 こちらからアクセスしてください。
- 情報源: https://quantum-journal.org/papers/q-2023-05-24-1021/
- :持っている
- :は
- :not
- :どこ
- ][p
- 1
- 10
- 11
- 12
- 13
- 14
- 視聴者の38%が
- 17
- 1934
- 1994
- 1998
- 1999
- 20
- 2001
- 2011
- 2012
- 2013
- 2014
- 2015
- 2016
- 2017
- 2019
- 2020
- 2021
- 2022
- 2023
- 22
- 23
- 24
- 26
- 27
- 28
- 30
- 39
- 40
- 49
- 50
- 60
- 7
- 8
- 84
- 87
- 9
- 91
- a
- 上記の.
- 抽象
- アカデミック
- アカデミー
- アクセス
- 正確にデジタル化
- 実際に
- 所属
- 後
- 前
- すべて
- また
- アメリカ
- an
- &
- どれか
- 適用された
- アプローチ
- です
- エリア
- アリゾナ州
- AS
- 著者
- 著者
- BE
- ビーム
- き
- バークリー
- 越えて
- ブラック
- ブラックホール
- 結合した
- ブレーク
- ブリュッセル
- 会報
- by
- カリフォルニア州
- ケンブリッジ
- 缶
- キャプチャー
- キャリー
- センター
- 世紀
- チャネル
- チャンネル
- 特徴づけます
- class
- コヒーレント
- カレッジ
- コメント
- コモンズ
- コミュニケーション
- 通信部
- 比較
- コンプリート
- 計算
- コンピュータ
- 懸念事項
- 結論
- 条件
- 講演
- 推測
- コンテキスト
- 連続的な
- 貢献
- 著作権
- 可能性
- データ
- それ
- デンマーク
- 密度
- 依存性
- 説明する
- 発展した
- 死
- 話し合います
- 議論
- ディストリビューション
- 発散
- 二重に
- ダイナミクス
- e
- 経済
- ed
- 環境
- 同等の
- 特に
- エーテル(ETH)
- 証拠
- 搾取
- 探る
- 探る
- 魅惑的な
- フィールズ
- フィッティング
- 発見
- 第4
- フレームワーク
- から
- function
- 機能
- 基本的な
- Games
- 世代
- グローバルに
- 陸上
- ハーバード
- 持ってる
- he
- こちら
- ヘルツ
- ホルダー
- 穴
- HTTPS
- i
- 識別
- IEEE
- 画像
- 意義
- in
- 不平等
- 不平等
- 情報
- 機関
- 興味深い
- 世界全体
- 紹介する
- IT
- ITS
- JavaScriptを
- ジャーナル
- 姓
- 後で
- 法制
- コメントを残す
- less
- ライセンス
- 光
- リスト
- 局部的に
- 最低
- 製
- メイン
- 作成
- マレーシアの
- マーティン
- 数学的
- 数学
- マトリックス
- 最大幅
- 五月..
- 手段
- だけど
- 測定結果
- 措置
- 力学
- メッセンジャー
- Michael Liebreich
- 最小
- マサチューセッツ工科大学(MIT)
- 混合
- モード
- モダン
- 弾み
- 月
- 他には?
- 最も
- すなわち
- 国
- 国民
- ナチュラル
- 決して
- 新作
- ニューヨーク
- ニコラス
- いいえ
- 特に
- 多数の
- of
- on
- ONE
- の
- 開いた
- オープンソース
- 演算子
- 光学
- 最適化
- or
- 注文
- オリジナル
- その他
- 私たちの
- 自分自身
- 出力
- が
- ペア
- 足
- 紙素材
- パラダイム
- 粒子
- パッシブ
- 相
- 物理的な
- 物理学
- プラトン
- プラトンデータインテリジェンス
- プラトデータ
- 位置
- 正の
- 電力
- 強力な
- 正確な
- 予測
- 保全
- 原則
- 確率
- Proceedings
- 処理
- 適切な
- プロパティ
- 受験する
- 提供します
- は、大阪で
- 公表
- 出版社
- 出版社
- 出版
- 目的
- Python
- 量
- 量子
- 量子もつれ
- 量子情報
- 量子光学
- 量子物理学
- 量子システム
- 測距
- 再編成
- 最近
- 最近
- リファレンス
- 参加申し込み
- 関係
- 関係
- 相対的に
- 関連した
- 残っている
- レポート
- 制限する
- 結果
- 結果
- レビュー
- レビュー
- 堅牢な
- 職種
- s
- 満足
- 科学
- 科学
- 二番
- 思われる
- センス
- シリーズ
- セッションに
- すべき
- 表示する
- 示す
- シグナル
- 簡単な拡張で
- 同時に
- 社会
- 一部
- スペース
- スピン
- 都道府県
- ステートメント
- 米国
- 統計
- 強い
- 首尾よく
- そのような
- 十分な
- 適当
- サポート
- シンポジウム
- システム
- 取り
- 技術的
- より
- それ
- アプリ環境に合わせて
- その後
- 理論的な
- 理論
- したがって、
- 彼ら
- この
- 三
- 役職
- 〜へ
- ツール
- に向かって
- 取引
- 変換
- true
- 順番
- ターニング
- type
- 不確かな
- 不確実性
- 下
- 理解する
- 理解された
- ユナイテッド
- 大学
- カリフォルニア大学
- ケンブリッジ大学
- 更新しました
- URL
- 中古
- 値
- さまざまな
- バージョン
- 非常に
- 、
- ボリューム
- の
- W
- 欲しいです
- ました
- ウェーブ
- we
- which
- while
- 作品
- X
- 年
- 年
- まだ
- ヨーク
- ゼファーネット