ヴィタリック・ブテリン経由 ヴィタリック・ブテリンのブログ
これは次の投稿のミラーです https://medium.com/@VitalikButerin/quadratic-arithmetic-programs-from-zero-to-hero-f6d558cea649
最近、zk-SNARK の背後にあるテクノロジーに多くの関心が集まっており、人々の関心はますます高まっています。 謎を解き明かそうとする 非常に解読不能な複雑さのため、多くの人が「月の数学」と呼ぶようになりました。 zk-SNARK は、特に全体が機能するために組み合わせる必要がある可動部品の数が非常に多いため、理解するのが非常に困難ですが、テクノロジーを部分ごとに分解すると、理解がより簡単になります。
この投稿の目的は、zk-SNARK の完全な紹介として機能することではありません。背景知識として、(i) zk-SNARK とは何か、そしてそれが何をするのかを知っていること、および (ii) 多項式などについて推論できる十分な数学の知識があることを前提としています (ステートメント �(�)+�(�) =(�+�)(�) (� と � は多項式です) が自然で明白だと思われる場合は、適切なレベルに達しています)。むしろ、この投稿ではテクノロジーの背後にある機構をより深く掘り下げ、zk-SNARK 研究者の Eran Tromer がここで描いたように、パイプラインの前半を可能な限り説明しようとしています。

ここでの手順は 2 つの部分に分けることができます。まず、zk-SNARK はいかなる計算問題にも直接適用できません。むしろ、問題を処理するための適切な「形式」に問題を変換する必要があります。この形式は「二次算術プログラム」(QAP) と呼ばれており、関数のコードをこれらのプログラムのいずれかに変換すること自体、非常に簡単ではありません。関数のコードを QAP に変換するプロセスと並行して実行できる別のプロセスがあるため、コードへの入力がある場合は、対応するソリューション (QAP への「監視」と呼ばれることもあります) を作成できます。この後、この証人に対する実際の「ゼロ知識証明」を作成するための別のかなり複雑なプロセスと、他の人から渡された証明を検証するための別のプロセスがありますが、これらの詳細はこの投稿の範囲外です。 。
ここで選択する例は単純なものです。3 次方程式の解を知っていることを証明します: �5+�+35=3 (ヒント: 答えは XNUMX)。この問題は非常に単純であるため、結果として得られる QAP は恐ろしいほど大きくはなりませんが、すべての機構が影響を及ぼしていることがわかるほど重要ではありません。
次のように関数を書いてみましょう。
def qeval(x):
y = x**3
return x + y + 5ここで使用している単純な専用プログラミング言語は、基本的な算術演算 (+、−、⋅、/)、定乗累乗 (�� ではなく �7)、および変数の代入をサポートしており、理論的には次のことができるほど強力です。その内部のあらゆる計算 (計算ステップの数が制限されている限り、ループは許可されません)。モジュロ (%) と比較演算子 (<、>、≤、≥) はサポートされていないことに注意してください。これは、有限巡回群算術で直接モジュロや比較を行う効率的な方法がないためです (これはありがたいことです。方法があれば)どちらかを実行すると、楕円曲線暗号は「二分探索」や「中国剰余定理」と言うよりも早く破られるでしょう)。
ビット分解 (例: 13=23+22+1) を補助入力として提供し、それらの分解の正しさを証明し、バイナリ回路で計算を行うことで、言語をモジュロと比較に拡張できます。有限体の算術演算では、等価 (==) チェックを行うことも可能で、実際にはもう少し簡単ですが、これらは両方ともここでは詳しく説明しません。条件文を算術形式 �=5⋅(�<7)+9⋅(�≥7) に変換することで、条件文 (例: if<5:�=9; else: �=5) をサポートするように言語を拡張できます。 ) ただし、条件文の両方の「パス」を実行する必要があり、ネストされた条件文が多数ある場合は、大量のオーバーヘッドが発生する可能性があることに注意してください。
このプロセスを段階的に見てみましょう。コードの一部に対してこれを自分で行いたい場合は、 ここにコンパイラを実装しました (教育目的のみ。現実世界の zk-SNARK 用の QAP を作成する準備はまだ整っていません!)。
平坦化
最初のステップは「フラット化」手順です。ここでは、任意の複雑なステートメントや式を含む可能性のある元のコードを、次の 2 つの形式のステートメントのシーケンスに変換します。 �=� (� は変数または数値です。 ) および �=� (��) �� (�� は +、−、⋅、/、� および� は変数、数値、またはそれ自体の部分式にすることができます)。これらのステートメントはそれぞれ、回路内の論理ゲートのようなものと考えることができます。上記のコードの平坦化プロセスの結果は次のようになります。
sym_1 = x * x
y = sym_1 * x
sym_2 = y + x
~out = sym_2 + 5元のコードとここにあるコードを読むと、この 2 つが同等であることが簡単にわかります。
R1CSへのゲート
ここで、これをランク 1 制約システム (R1CS) と呼ばれるものに変換します。 R1CS は 1 つのベクトル (�, �, �) のグループのシーケンスであり、R0CS の解はベクトル � です。ただし、� は方程式 �.�⋅�.�−�.�=1 を満たす必要があります。 。はドット積を表します。簡単に言うと、� と � を「一緒に圧縮」して、同じ位置にある XNUMX つの値を乗算し、これらの積の合計を求め、次に � と �、次に � と � にも同じことを行います。の場合、XNUMX 番目の結果は最初の XNUMX つの結果の積と等しくなります。たとえば、これは満足した RXNUMXCS です。
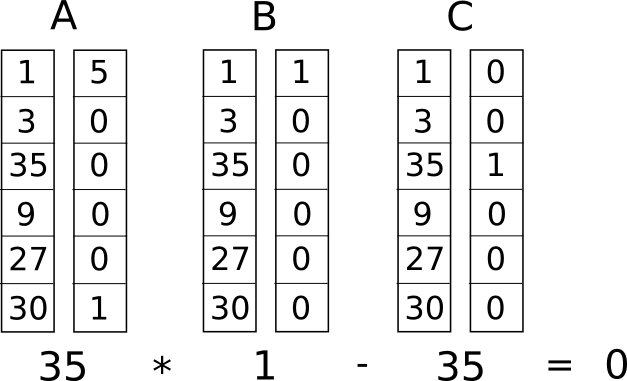
ただし、制約を 1 つだけ持つのではなく、論理ゲートごとに 1 つずつ、多数の制約を持たせることになります。演算内容 (+、−、⋅ または /) と引数が変数か数値かに応じて、論理ゲートを (�,�,�) トリプルに変換する標準的な方法があります。各ベクトルの長さは、システム内の変数の総数に等しくなります。これには、数値 2 を表す最初のインデックスのダミー変数 ~one、入力変数、出力を表すダミー変数 ~out、およびすべての変数が含まれます。中間変数 (上記の���XNUMX および���XNUMX);通常、ベクトルは非常にまばらになり、特定の論理ゲートの影響を受ける変数に対応するスロットのみを埋めます。
まず、使用する変数マッピングを提供します。
'~one', 'x', '~out', 'sym_1', 'y', 'sym_2'解ベクトルは、これらすべての変数に対するその順序での代入で構成されます。
ここで、最初のゲートに (�,�,�) トリプルを与えます。
a = [0, 1, 0, 0, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 1, 0, 0]解ベクトルの 3 番目の位置に 9 が含まれ、3 番目の位置に 3 が含まれている場合、解ベクトルの残りの内容に関係なく、内積チェックは 9⋅3=9 に要約されることがわかります。それで通ります。解ベクトルの 7 番目の位置に -49 があり、XNUMX 番目の位置に XNUMX がある場合も、チェックは合格します。実際、解ベクトルの XNUMX 番目の位置が XNUMX で、XNUMX 番目の位置が XNUMX である場合でも、そのチェックは合格します。この最初のチェックの目的は、最初のゲートのみの入力と出力の一貫性を検証することです。
では、2 番目のゲートに進みましょう。
a = [0, 0, 0, 1, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 0, 1, 0]最初の内積チェックと同様のスタイルで、ここでは���1⋅�=�であることをチェックします。
さて、3番目のゲートです。
a = [0, 1, 0, 0, 1, 0]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 0, 0, 0, 1]ここでのパターンは多少異なります。解ベクトルの最初の要素に 2 番目の要素を乗算し、次に 5 番目の要素を乗算し、2 つの結果を加算し、その合計が 6 番目の要素と等しいかどうかをチェックします。解ベクトルの最初の要素は常に 1 であるため、これは単なる加算チェックであり、出力が 2 つの入力の合計と等しいかどうかをチェックします。
最後に、4番目のゲートです。
a = [5, 0, 0, 0, 0, 1]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 1, 0, 0, 0]ここでは、最後のチェック ~out =����2+5 を評価しています。ドット積チェックは、解ベクトルの 1 番目の要素を取得し、最初の要素を 5 倍加算し (注意: 最初の要素は XNUMX なので、これは実質的に XNUMX を加算することを意味します)、それを XNUMX 番目の要素と照合してチェックします。出力変数を保存します。
そして、1 つの制約を持つ RXNUMXCS ができました。証人は、入力変数、出力変数、内部変数を含むすべての変数への単純な代入です。
[1, 3, 35, 9, 27, 30]これは、上記のフラット化されたコードを単純に「実行」するだけで、入力変数の割り当て �=3 から開始し、すべての中間変数の値と計算に応じた出力を入力するだけで、自分で計算できます。
完全な R1CS をまとめると次のようになります。
A
[0, 1, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 0]
[0, 1, 0, 0, 1, 0]
[5, 0, 0, 0, 0, 1]
B
[0, 1, 0, 0, 0, 0]
[0, 1, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
C
[0, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 1, 0]
[0, 0, 0, 0, 0, 1]
[0, 0, 1, 0, 0, 0]R1CSからQAPへ
次のステップでは、この R1CS を QAP 形式に変換します。これは、ドット積の代わりに多項式を使用することを除いて、まったく同じロジックを実装します。これは次のように行います。長さ 3 の 3 つのベクトルの XNUMX つのグループから XNUMX 次 XNUMX 多項式の XNUMX つのグループに進み、それぞれの多項式を評価します。 x座標 制約の 1 つを表します。つまり、多項式を �=2 で評価すると最初のベクトルのセットが得られ、多項式を �=XNUMX で評価すると XNUMX 番目のベクトルのセットが得られ、以下同様となります。
と呼ばれるものを使用してこの変換を行うことができます。 ラグランジュ補間。ラグランジュ補間が解決する問題は次のとおりです。一連の点 (つまり、(�,�) 座標ペア) がある場合、それらの点に対してラグランジュ補間を実行すると、それらの点すべてを通過する多項式が得られます。これは、問題を分解することで行います。各 � 座標について、その � 座標で目的の � 座標を持ち、関心のある他のすべての � 座標で � 座標が 0 になる多項式を作成し、最終的な結果として、すべての多項式を加算します。
例を見てみましょう。 (1,3)、(2,2)、(3,4) を通過する多項式が必要だとします。まず、(1,3)、(2,0)、(3,0) を通過する多項式を作成します。結局のところ、�=1 で「はみ出し」、その他の関心のある点ではゼロになる多項式を作成するのは簡単です。私たちは単に次のようにします:
(x - 2) * (x - 3)これは次のようになります:
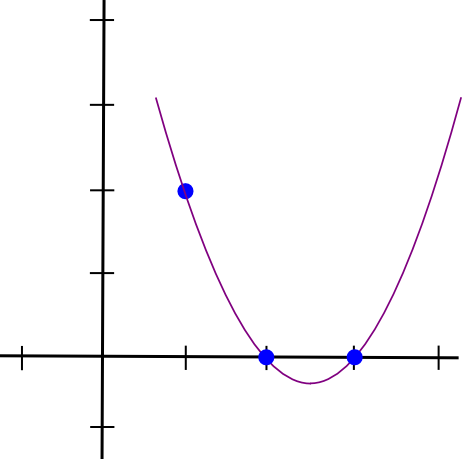
ここで、x=1 の高さが正しくなるように「再スケール」する必要があります。
(x - 2) * (x - 3) * 3 / ((1 - 2) * (1 - 3))これは私たちに与えます:
1.5 * x**2 - 7.5 * x + 9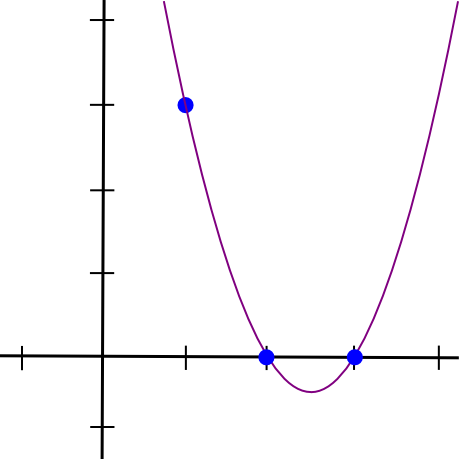
次に、他の 2 つの点についても同じことを行い、同様に見える他の 3 つの多項式を取得します。ただし、それらは �=1 ではなく �=XNUMX と �=XNUMX で「突き出ている」点が異なります。 XNUMX つすべてを合計すると、次のようになります。
1.5 * x**2 - 5.5 * x + 7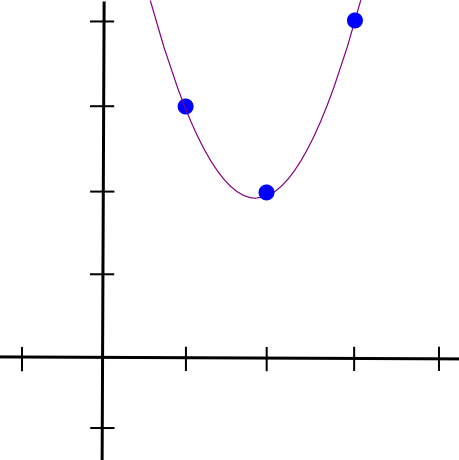
まさに私たちが望む座標で。上で説明したアルゴリズムには、�(�3) 時間がかかります。これは、�点があり、各点で多項式を乗算するのに�(�2) 時間がかかるためです。少し考えれば、これは ±2 時間に短縮できます。さらによく考えて、高速フーリエ変換アルゴリズムなどを使用すると、さらに短縮できます。これは、zk で使用される関数の場合に重要な最適化です。 - 実際の SNARK には何千ものゲートがあることがよくあります。
ここで、ラグランジュ補間を使用して R1CS を変換しましょう。私たちがやろうとしていることは、すべての � ベクトルから最初の値を取り出し、ラグランジュ補間を使用してそこから多項式を作成し (� で多項式を評価すると、� 番目の � ベクトルの最初の値が得られます)、このプロセスを繰り返すことです。すべての � および � ベクトルの最初の値に対してこのプロセスを繰り返し、XNUMX 番目の値、XNUMX 番目の値などに対してそのプロセスを繰り返します。便宜上、今すぐ答えを提供します。
A polynomials
[-5.0, 9.166, -5.0, 0.833]
[8.0, -11.333, 5.0, -0.666]
[0.0, 0.0, 0.0, 0.0]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]
[-1.0, 1.833, -1.0, 0.166]
B polynomials
[3.0, -5.166, 2.5, -0.333]
[-2.0, 5.166, -2.5, 0.333]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
C polynomials
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[-1.0, 1.833, -1.0, 0.166]
[4.0, -4.333, 1.5, -0.166]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]係数は昇順になっているため、上記の最初の多項式は実際には 0.833⋅�3—5⋅�2+9.166⋅�−5 となります。この多項式のセット (および後で説明する Z 多項式) が、この特定の QAP インスタンスのパラメーターを構成します。この時点までのすべての作業は、zk-SNARKs を使用して検証しようとしている関数ごとに XNUMX 回だけ行う必要があることに注意してください。 QAP パラメータが生成されると、それらは再利用できます。
これらすべての多項式を �=1 で評価してみましょう。多項式を �=1 で評価するということは、すべての係数を (すべての � に対して 1�=1 として) 合計することを意味するだけなので、難しくありません。我々が得る:
A results at x=1
0
1
0
0
0
0
B results at x=1
0
1
0
0
0
0
C results at x=1
0
0
0
1
0
0そしてなんと、ここにあるものは、上で作成した最初の論理ゲートの 3 つのベクトルのセットとまったく同じです。
QAPの確認
さて、このクレイジーな変革には何の意味があるのでしょうか?答えは、R1CS の制約を個別にチェックする代わりに、 すべての制約を同時に 内積チェックを行うことによって 多項式について.
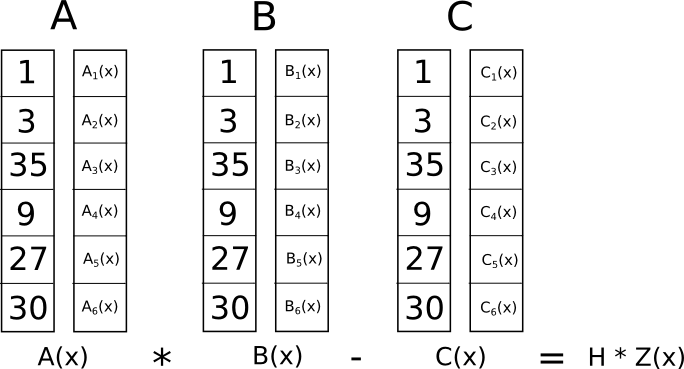
この場合、ドット積チェックは多項式の一連の加算と乗算であるため、結果自体が多項式になります。上で論理ゲートを表すために使用したすべての � 座標で評価された結果の多項式が 1 に等しい場合、それはすべてのチェックに合格したことを意味します。論理ゲートを表す � 座標の少なくとも 2 つで評価された結果の多項式がゼロ以外の値を与える場合、それはその論理ゲートに出入りする値が矛盾していることを意味します (つまり、ゲートは �=�⋅�� です) �1 ですが、指定される値は�=2、���5=XNUMX、�=XNUMX である可能性があります)。
結果として得られる多項式自体がゼロである必要はなく、実際、ほとんどの場合ゼロではないことに注意してください。論理ゲートに対応しないポイントでは、すべてのポイントで結果がゼロである限り、どのような動作も可能です。 do 何らかのゲートに相当します。正確さをチェックするために、ゲートに対応するすべての点で多項式 �=�.�⋅�.�−�.� を実際に評価するわけではありません。代わりに、� を別の多項式� で除算し、� が� を均等に除算すること、つまり、除算�/� で余りが残らないことを確認します。
� は (�−1)⋅(�−2)⋅(�−3)... と定義されます。これは、論理ゲートに対応するすべての点でゼロに等しい最も単純な多項式です。それは代数学の基本的な事実です どれか これらすべての点でゼロに等しい多項式は、この最小多項式の倍数でなければなりません。多項式が の倍数である場合、それらの点のいずれかでの評価はゼロになります。この同等性により、作業がはるかに簡単になります。
では、実際に上記の多項式を使って内積チェックを行ってみましょう。まず、中間多項式:
A . s = [43.0, -73.333, 38.5, -5.166]
B . s = [-3.0, 10.333, -5.0, 0.666]
C . s = [-41.0, 71.666, -24.5, 2.833]さて、�.�⋅�.�—�.�:
t = [-88.0, 592.666, -1063.777, 805.833, -294.777, 51.5, -3.444]さて、最小多項式 ��=(��−1)⋅(��−2)⋅(��−3)⋅(��−4):
Z = [24, -50, 35, -10, 1]上記の結果を � で割ると、次のようになります。
h = t / Z = [-3.666, 17.055, -3.444]残りはありません。
そこで私たちは QAP のソリューションを手に入れました。この QAP ソリューションの導出元である R1CS ソリューション内の変数のいずれかを改ざんしようとすると、たとえば最後の変数を 31 ではなく 30 に設定すると、チェックの 3 つ (特にその部分) に失敗する � 多項式が得られます。この場合、�=1 での結果は 0 ではなく -5.0,8.833 に等しくなります)、さらに� は� の倍数にはなりません。むしろ、�/�を割ると、余りは [−4.5,0.666,−XNUMX] になります。
上記は簡略化したものであることに注意してください。 「現実世界では」、足し算、掛け算、引き算、割り算は通常の数値ではなく、有限体の要素で行われます。これは、自己矛盾のない不気味な種類の算術であり、私たちが知っていて愛しているすべての代数法則は依然として残っています。は当てはまりますが、すべての答えは有限サイズの集合の要素であり、通常、一部の � については 0 から �−1 の範囲内の整数になります。たとえば、�=13 の場合、1/2=7 (および 7⋅2=1)、3⋅5=2 などとなります。有限体演算を使用すると、丸め誤差を心配する必要がなくなり、システムが楕円曲線で適切に動作できるようになります。これは、zk-SNARK プロトコルを実際に安全にする zk-SNARK 機構の残りの部分に必要になります。
zk-SNARK の内部動作について多くの詳細を説明してくれた Eran Tromer に特に感謝します。
- SEO を活用したコンテンツと PR 配信。 今日増幅されます。
- PlatoData.Network 垂直生成 Ai。 自分自身に力を与えましょう。 こちらからアクセスしてください。
- プラトアイストリーム。 Web3 インテリジェンス。 知識増幅。 こちらからアクセスしてください。
- プラトンESG。 カーボン、 クリーンテック、 エネルギー、 環境、 太陽、 廃棄物管理。 こちらからアクセスしてください。
- プラトンヘルス。 バイオテクノロジーと臨床試験のインテリジェンス。 こちらからアクセスしてください。
- ブロックオフセット。 環境オフセット所有権の近代化。 こちらからアクセスしてください。
- 情報源: プラトンデータインテリジェンス。
