[מראה] תוכניות אריתמטיקה ריבועית: מאפס לגיבור

Vitalik Buterin דרך ה בלוג ויטליק בוטרין

זוהי מראה של הפוסט ב https://medium.com/@VitalikButerin/quadratic-arithmetic-programs-from-zero-to-hero-f6d558cea649

לאחרונה הייתה עניין רב בטכנולוגיה שמאחורי zk-SNARKs, ואנשים הולכים ומתרבים מנסה לעשות דה-מיסטיציה משהו שרבים קראו לו "מתמטיקה ירח" בשל המורכבות הבלתי ניתנת לפענוח שלו. zk-SNARKs הם אכן די מאתגרים לתפיסה, במיוחד בשל המספר העצום של חלקים נעים שצריכים להתאחד כדי שהעניין כולו יעבוד, אבל אם נשבור את הטכנולוגיה חלק אחר חלק אז ההבנה של זה הופכת לפשוטה יותר.

מטרת פוסט זה אינה לשמש כהקדמה מלאה ל-zk-SNARKs; הוא מניח כידע רקע ש(i) אתה יודע מה הם zk-SNARKs ומה הם עושים, ו-(ii) יודע מספיק מתמטיקה כדי להיות מסוגל לנמק דברים כמו פולינומים (אם ההצהרה �(�)+�(�) =(�+�)(�) , כאשר � ו� הם פולינומים, נראה לך טבעי ומובן מאליו, אז אתה ברמה הנכונה). במקום זאת, הפוסט חופר עמוק יותר במכונות שמאחורי הטכנולוגיה, ומנסה להסביר טוב ככל האפשר את המחצית הראשונה של הצינור, כפי שצייר חוקר zk-SNARK ערן טרומר כאן:

את השלבים כאן ניתן לחלק לשני חצאים. ראשית, לא ניתן להחיל zk-SNARKs על שום בעיה חישובית ישירות; במקום זאת, עליך להמיר את הבעיה ל"צורה" הנכונה כדי שהבעיה תוכל לפעול. הצורה נקראת "תוכנית אריתמטית ריבועית" (QAP), והפיכת הקוד של פונקציה לאחד מאלה היא בעצמה מאוד לא טריוויאלית. יחד עם תהליך המרת הקוד של פונקציה ל-QAP יש תהליך נוסף שניתן להריץ לצדו כך שאם יש לך קלט לקוד תוכל ליצור פתרון מתאים (נקרא לפעמים "עד" ל-QAP). לאחר מכן, ישנו עוד תהליך מורכב למדי ליצירת "הוכחת אפס ידע" בפועל עבור העד הזה, ותהליך נפרד לאימות הוכחה שמישהו אחר מעביר אליך, אך אלו פרטים שאינם בגדר הפוסט הזה. .

הדוגמה שנבחר היא פשוטה: הוכחה שאתה יודע את הפתרון למשוואה מעוקבת: �3+�+5=35 (רמז: התשובה היא 3). הבעיה הזו פשוטה מספיק כדי שה-QAP שיתקבל לא יהיה כל כך גדול עד כדי אימה, אבל לא טריוויאלי מספיק כדי שתוכל לראות את כל המכונות נכנסות לפעולה.

הבה נכתוב את הפונקציה שלנו באופן הבא:

def qeval(x):
    y = x**3
    return x + y + 5

שפת התכנות הפשוטה למטרות מיוחדות שבה אנו משתמשים כאן תומכת באריתמטיקה בסיסית (+, −, ⋅, /), הערכת הספק קבוע (�7 אך לא ��) והקצאת משתנה, שהיא מספיק חזקה שתוכל לעשות באופן תיאורטי. כל חישוב בתוכו (כל עוד מספר השלבים החישוביים מוגבל; אין לולאות מותרות). שימו לב שמודולו (%) ואופרטורי השוואה (<, >, ≤, ≥) אינם נתמכים, מכיוון שאין דרך יעילה לבצע מודולו או השוואה ישירות באריתמטיקה של קבוצות מחזוריות סופית (תודה על כך; אם הייתה דרך כדי לבצע אחת מהן, אז קריפטוגרפיה של עקומה אליפטית תישבר מהר יותר ממה שאתה יכול לומר "חיפוש בינארי" ו"משפט שאריות סינית").

אתה יכול להרחיב את השפה למודולו והשוואות על ידי מתן פירוק סיביות (למשל 13=23+22+1) ככניסות עזר, הוכחת נכונות הפירוקים הללו וביצוע מתמטיקה במעגלים בינאריים; בחשבון שדה סופי, ביצוע בדיקות שוויון (==) הוא גם בר ביצוע ולמעשה קצת יותר קל, אבל אלה שני פרטים שלא ניכנס אליהם כרגע. אנו יכולים להרחיב את השפה לתמיכה בתנאים (למשל אם �<5:�=7; אחר: �=9) על ידי המרתם לצורה אריתמטית: �=7⋅(�<5)+9⋅(�≥5 ) אם כי שים לב ששני ה"נתיבים" של התנאי יצטרכו להתבצע, ואם יש לך תנאים מקוננים רבים אז זה יכול להוביל לכמות גדולה של תקורה.

הבה נעבור כעת את התהליך הזה צעד אחר צעד. אם אתה רוצה לעשות זאת בעצמך עבור כל פיסת קוד, אני הטמיע כאן מהדר (למטרות חינוכיות בלבד; עדיין לא מוכן ליצור QAPs עבור zk-SNARKs בעולם האמיתי!).

השטחה

השלב הראשון הוא הליך "שיטוח", שבו אנו ממירים את הקוד המקורי, שעשוי להכיל הצהרות וביטויים מורכבים באופן שרירותי, לרצף של הצהרות בשתי צורות: �=� (כאשר � יכול להיות משתנה או מספר ) ו- �=� (��) � (כאשר �� יכול להיות +, −, ⋅, / ו- � ו- � יכולים להיות משתנים, מספרים או תתי-ביטויים עצמם). אתה יכול לחשוב על כל אחד מההצהרות האלה כמו סוג של שערים לוגיים במעגל. התוצאה של תהליך הרידוד עבור הקוד לעיל היא כדלקמן:

sym_1 = x * x
y = sym_1 * x
sym_2 = y + x
~out = sym_2 + 5

אם תקרא את הקוד המקורי ואת הקוד כאן, אתה יכול די בקלות לראות שהשניים שווים.

שערים ל-R1CS

כעת, אנו ממירים את זה למשהו שנקרא מערכת אילוצים דרגה 1 (R1CS). R1CS הוא רצף של קבוצות של שלושה וקטורים (�, �, �), והפתרון ל-R1CS הוא וקטור �, כאשר � חייב לעמוד במשוואה �.�⋅�.�−�.�=0, כאשר . מייצג את מוצר הנקודה - במונחים פשוטים יותר, אם "נכון יחד" � ו- , נכפיל את שני הערכים באותם מיקומים, ולאחר מכן ניקח את סכום המוצרים הללו, ואז נעשה אותו דבר ל- � ו- � ואז � ו- � , אז התוצאה השלישית שווה למכפלה של שתי התוצאות הראשונות. לדוגמה, זהו R1CS מרוצה:

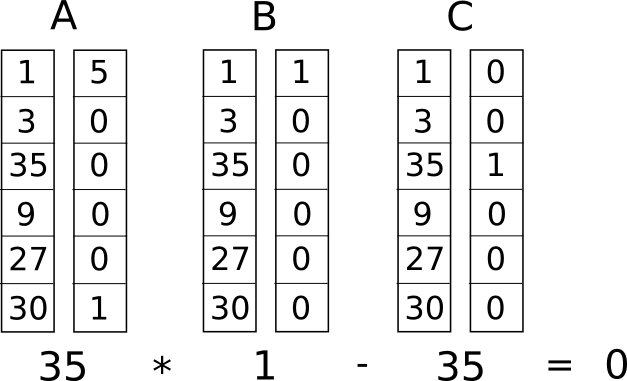
אבל במקום שיהיה לנו רק אילוץ אחד, יהיו לנו אילוצים רבים: אחד לכל שער לוגי. ישנה דרך סטנדרטית להמיר שער לוגי לטריפל (�,�,�) תלוי מה הפעולה (+, −, ⋅ או /) והאם הארגומנטים הם משתנים או מספרים. אורכו של כל וקטור שווה למספר המשתנים הכולל במערכת, כולל משתנה דמה ~אחד באינדקס הראשון המייצג את המספר 1, משתני הקלט, משתנה דמה ~out המייצג את הפלט, ולאחר מכן כל משתני ביניים (���1 ו���2 לעיל); הווקטורים בדרך כלל יהיו דלילים מאוד, רק ימלאו את החריצים המתאימים למשתנים המושפעים משער לוגי מסוים.

ראשית, נספק את מיפוי המשתנה שבו נשתמש:

'~one', 'x', '~out', 'sym_1', 'y', 'sym_2'

וקטור הפתרון יהיה מורכב מהקצאות עבור כל המשתנים הללו, בסדר זה.

כעת, ניתן את המשולש (�,�,�) עבור השער הראשון:

a = [0, 1, 0, 0, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 1, 0, 0]

ניתן לראות שאם וקטור הפתרון מכיל 3 במיקום השני, ו-9 במיקום הרביעי, אז ללא קשר לשאר התוכן של וקטור הפתרון, בדיקת המוצר הנקודה תסתכם ל-3⋅3=9, ו אז זה יעבור. אם לוקטור הפתרון יש −3 במיקום השני ו-9 במיקום הרביעי, גם הסימון יעבור; למעשה, אם לוקטור הפתרון יש 7 במיקום השני ו-49 בעמדה הרביעית אז הבדיקה הזו עדיין תעבור - מטרת הבדיקה הראשונה הזו היא לאמת את העקביות של הכניסות והיציאות של השער הראשון בלבד.

כעת, נמשיך לשער השני:

a = [0, 0, 0, 1, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 0, 1, 0]

בסגנון דומה לבדיקת המוצר הנקודה הראשונה, כאן אנו בודקים ש���1⋅�=�.

עכשיו, השער השלישי:

a = [0, 1, 0, 0, 1, 0]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 0, 0, 0, 1]

כאן, התבנית שונה במקצת: היא מכפילה את האלמנט הראשון בווקטור הפתרון באלמנט השני, ואז באלמנט החמישי, הוספת שתי התוצאות ובודקים אם הסכום שווה לאלמנט השישי. מכיוון שהאלמנט הראשון בווקטור הפתרון הוא תמיד אחד, זה רק בדיקת חיבור, הבודקת שהפלט שווה לסכום שתי התשומות.

לבסוף, השער הרביעי:

a = [5, 0, 0, 0, 0, 1]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 1, 0, 0, 0]

כאן, אנו מעריכים את הצ'ק האחרון, ~out =���2+5. בדיקת מוצר הנקודה פועלת על ידי לקיחת האלמנט השישי בווקטור הפתרון, הוספת חמש פעמים מהאלמנט הראשון (תזכורת: האלמנט הראשון הוא 1, אז זה אומר למעשה הוספת 5), ובדיקתו מול האלמנט השלישי, שם אנו לאחסן את משתנה הפלט.

ושם יש לנו את ה-R1CS שלנו עם ארבעה אילוצים. העד הוא פשוט ההקצאה לכל המשתנים, כולל קלט, פלט ומשתנים פנימיים:

[1, 3, 35, 9, 27, 30]

אתה יכול לחשב זאת בעצמך פשוט על ידי "ביצוע" הקוד השטוח למעלה, התחל עם הקצאת משתנה הקלט �=3, והכנסת הערכים של כל משתני הביניים והפלט תוך כדי חישובם.

ה-R1CS המלא ביחד הוא:

A
[0, 1, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 0]
[0, 1, 0, 0, 1, 0]
[5, 0, 0, 0, 0, 1]

B
[0, 1, 0, 0, 0, 0]
[0, 1, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]

C
[0, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 1, 0]
[0, 0, 0, 0, 0, 1]
[0, 0, 1, 0, 0, 0]

R1CS ל-QAP

השלב הבא הוא לקחת את ה-R1CS הזה ולהמיר אותו לצורת QAP, המיישמת את אותו היגיון בדיוק למעט שימוש בפולינומים במקום במוצרי נקודות. אנו עושים זאת כדלקמן. אנו עוברים 3מארבע קבוצות של שלושה וקטורים באורך שש עד שש קבוצות של שלוש מעלות-3 פולינומים, כאשר מעריכים את הפולינומים בכל קואורדינטת x מייצג את אחד האילוצים. כלומר, אם אנו מעריכים את הפולינומים ב- �=1, אז נקבל את קבוצת הוקטורים הראשונה שלנו, אם אנו מעריכים את הפולינומים ב-�=2, אז נקבל את קבוצת הווקטורים השנייה שלנו, וכן הלאה.

אנחנו יכולים לעשות את השינוי הזה באמצעות משהו שנקרא a אינטרפולציה של לגראנז'. הבעיה שאינטרפולציה של לגראנז' פותרת היא זו: אם יש לך קבוצה של נקודות (כלומר (�,�) זוגות קואורדינטות), אז ביצוע אינטרפולציה של Lagrange בנקודות האלה נותן לך פולינום שעובר דרך כל הנקודות הללו. אנו עושים זאת על ידי פירוק הבעיה: עבור כל קואורדינטה, אנו יוצרים פולינום שיש לו את הקואורדינטה הרצויה באותה קואורדינטה ו- קואורדינטה של ​​0 בכל הקואורדינטות האחרות שאנו מעוניינים בהן, ולאחר מכן כדי לקבל את הסופי התוצאה נוסיף את כל הפולינומים יחד.

בואו נעשה דוגמה. נניח שאנו רוצים פולינום שעובר דרך (1,3),(2,2) ו-(3,4). נתחיל ביצירת פולינום שעובר דרך (1,3),(2,0) ו-(3,0). כפי שמתברר, קל ליצור פולינום ש"בולט" ב- �=1 והוא אפס בנקודות העניין האחרות; אנחנו פשוט עושים:

(x - 2) * (x - 3)

שנראה כך:

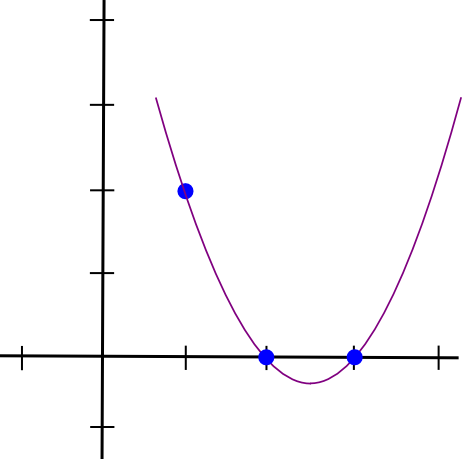
כעת, אנחנו רק צריכים "לשנות את קנה המידה" כך שהגובה ב-x=1 יהיה נכון:

(x - 2) * (x - 3) * 3 / ((1 - 2) * (1 - 3))

זה נותן לנו:

1.5 * x**2 - 7.5 * x + 9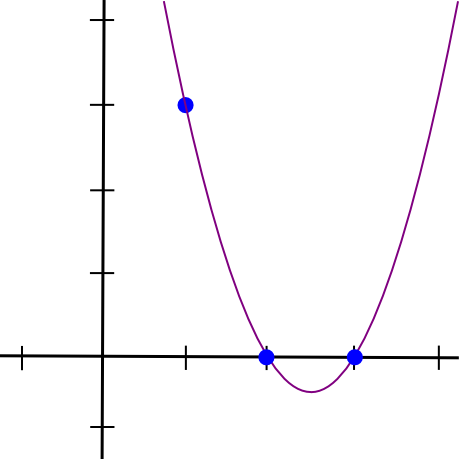

לאחר מכן נעשה את אותו הדבר עם שתי הנקודות האחרות, ונקבל שני פולינומים אחרים בעלי מראה דומה, אלא שהם "בולטים" ב-�=2 ו-�=3 במקום �=1. נוסיף את שלושתם יחד ונקבל:

1.5 * x**2 - 5.5 * x + 7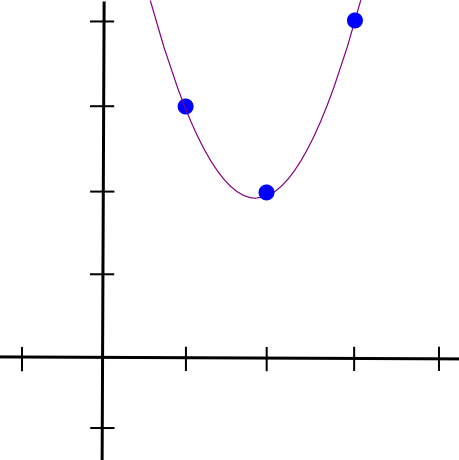

בדיוק עם הקואורדינטות שאנחנו רוצים. האלגוריתם כפי שתואר לעיל לוקח �(�3) זמן, מכיוון שיש � נקודות וכל נקודה דורשת �(�2) זמן כדי להכפיל את הפולינומים יחד; עם קצת חשיבה, ניתן לצמצם את זה ל-(�2) זמן, ועם הרבה יותר חשיבה, באמצעות אלגוריתמים מהירים של טרנספורמציה פורייה וכדומה, ניתן לצמצם אותו עוד יותר - אופטימיזציה מכרעת כאשר פונקציות שמתרגלות ב-zk -SNARKs בפועל יש לרוב אלפים רבים של שערים.

כעת, בואו נשתמש באינטרפולציה של לגראנז' כדי לשנות את ה-R1CS שלנו. מה שאנחנו הולכים לעשות זה לקחת את הערך הראשון מכל וקטור, להשתמש באינטרפולציה של לגראנז' כדי ליצור מזה פולינום (כאשר הערכת הפולינום ב- תקבל את הערך הראשון של הווקטור ה-), חזור על התהליך עבור הערך הראשון של כל וקטור � ו- �, ולאחר מכן חזור על התהליך הזה עבור הערכים השני, הערכים השלישי, וכן הלאה. מטעמי נוחות אספק את התשובות כבר עכשיו:

A polynomials
[-5.0, 9.166, -5.0, 0.833]
[8.0, -11.333, 5.0, -0.666]
[0.0, 0.0, 0.0, 0.0]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]
[-1.0, 1.833, -1.0, 0.166]

B polynomials
[3.0, -5.166, 2.5, -0.333]
[-2.0, 5.166, -2.5, 0.333]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]

C polynomials
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[-1.0, 1.833, -1.0, 0.166]
[4.0, -4.333, 1.5, -0.166]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]

המקדמים הם בסדר עולה, כך שהפולינום הראשון למעלה הוא למעשה 0.833⋅�3-5⋅�2+9.166⋅�−5. קבוצת פולינומים זו (בתוספת פולינום Z שאסביר בהמשך) מרכיבה את הפרמטרים עבור מופע QAP הספציפי הזה. שים לב שכל העבודה עד לנקודה זו צריכה להיעשות רק פעם אחת עבור כל פונקציה שאתה מנסה להשתמש ב-zk-SNARKs כדי לאמת; לאחר יצירת פרמטרי QAP, ניתן לעשות בהם שימוש חוזר.

בוא ננסה להעריך את כל הפולינומים האלה ב-�=1. הערכת פולינום ב- �=1 פירושה פשוט חיבור כל המקדמים (כ- 1�=1 עבור כל �), כך שזה לא קשה. אנחנו מקבלים:

A results at x=1
0
1
0
0
0
0

B results at x=1
0
1
0
0
0
0

C results at x=1
0
0
0
1
0
0

והנה, מה שיש לנו כאן זהה בדיוק לקבוצה של שלושה וקטורים לשער ההיגיון הראשון שיצרנו למעלה.

בדיקת QAP

עכשיו מה הטעם בשינוי המטורף הזה? התשובה היא שבמקום לבדוק את האילוצים ב-R1CS בנפרד, אנחנו יכולים כעת לבדוק כל האילוצים בו זמנית על ידי ביצוע בדיקת המוצר הנקודה על הפולינומים.

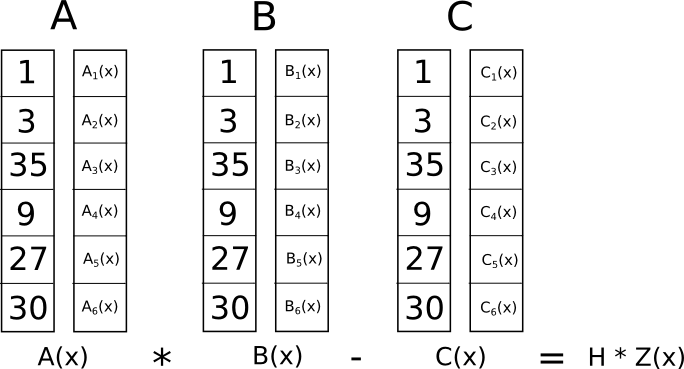
מכיוון שבמקרה זה בדיקת תוצר הנקודה היא סדרה של הוספות והכפלות של פולינומים, התוצאה עצמה הולכת להיות פולינום. אם הפולינום המתקבל, המוערך בכל קואורדינטה שבה השתמשנו לעיל כדי לייצג שער לוגי, שווה לאפס, אז זה אומר שכל הבדיקות עוברות; אם הפולינום המתקבל המוערך לפחות באחת מהקואורדינטות � המייצגות שער לוגי נותן ערך שאינו אפס, אז זה אומר שהערכים הנכנסים ויוצאים ממנו השער הלוגי אינם עקביים (כלומר, השער הוא �=�⋅�� �1 אך הערכים שסופקו עשויים להיות �=2,���1=2 ו-�=5).

שימו לב שהפולינום המתקבל לא חייב להיות אפס, ולמעשה ברוב המקרים לא יהיה זה; יכולה להיות לו כל התנהגות בנקודות שאינן תואמות לשערים לוגיים כל עוד התוצאה היא אפס בכל הנקודות do מתאים לשער כלשהו. כדי לבדוק נכונות, אנחנו לא מעריכים את הפולינום �=�.�⋅�.�−�.� בכל נקודה המתאימה לשער; במקום זאת, אנו מחלקים � בפולינום אחר, �, ובודקים ש� מחלק � באופן שווה – כלומר החלוקה �/� לא משאירה שארית.

� מוגדר כ-(�−1)⋅(�−2)⋅(�−3)... - הפולינום הפשוט ביותר ששווה לאפס בכל הנקודות המתאימות לשערים לוגיים. זוהי עובדה בסיסית באלגברה ש כל פולינום השווה לאפס בכל הנקודות הללו חייב להיות כפולה של הפולינום המינימלי הזה, ואם פולינום הוא כפולה של � אז ההערכה שלו בכל אחת מהנקודות הללו תהיה אפס; השקילות הזו הופכת את העבודה שלנו להרבה יותר קלה.

כעת, בוא נעשה את בדיקת המוצר הנקודה עם הפולינומים שלמעלה. ראשית, פולינומי הביניים:

A . s = [43.0, -73.333, 38.5, -5.166]
B . s = [-3.0, 10.333, -5.0, 0.666]
C . s = [-41.0, 71.666, -24.5, 2.833]

עכשיו, �.�⋅�.�—�.�:

t = [-88.0, 592.666, -1063.777, 805.833, -294.777, 51.5, -3.444]

כעת, הפולינום המינימלי �=(�−1)⋅(�−2)⋅(�−3)⋅(�−4):

Z = [24, -50, 35, -10, 1]

ואם נחלק את התוצאה למעלה ב�, נקבל:

h = t / Z = [-3.666, 17.055, -3.444]

בלי שארית.

וכך יש לנו את הפתרון ל-QAP. אם ננסה לזייף אחד מהמשתנים בפתרון R1CS שממנו אנו גוזרים את פתרון ה-QAP הזה - נניח, הגדר את האחרון ל-31 במקום 30, אז נקבל � פולינום שנכשל באחת הבדיקות (בפרט זה במקרה, התוצאה ב- �=3 תהיה שווה ל-1 במקום 0), ויתרה מכך � לא תהיה כפולה של �; במקום זאת, חלוקה של �/� תיתן שארית של [−5.0,8.833,−4.5,0.666].

שימו לב שהאמור לעיל הוא פשטנות; "בעולם האמיתי", החיבור, הכפל, החיסור והחילוק יתרחשו לא עם מספרים רגילים, אלא עם רכיבי שדה סופיים - סוג מפחיד של אריתמטיקה שתואמת את עצמה, כך שכל החוקים האלגבריים שאנו מכירים ואוהבים עדיין נכון, אבל כאשר כל התשובות הן רכיבים של קבוצה בגודל סופי, בדרך כלל מספרים שלמים בטווח שבין 0 ל- 1 עבור חלק מה �. לדוגמה, אם �=13, אז 1/2=7 (ו-7⋅2=1),3⋅5=2, וכן הלאה. שימוש באריתמטיקה של שדה סופי מסיר את הצורך לדאוג לשגיאות עיגול ומאפשר למערכת לעבוד בצורה יפה עם עקומות אליפטיות, שבסופו של דבר נחוצות עבור שאר מכונות zk-SNARK שהופכות את פרוטוקול zk-SNARK לאבטח למעשה.

תודה מיוחדת לערן טרומר על שעזר להסביר לי פרטים רבים על פעולתם הפנימית של zk-SNARKs.

• הפצת תוכן ויחסי ציבור מופעל על ידי SEO. קבל הגברה היום.
• PlatoData.Network Vertical Generative Ai. העצים את עצמך. גישה כאן.
• PlatoAiStream. Web3 Intelligence. הידע מוגבר. גישה כאן.
• PlatoESG. פחמן, קלינטק, אנרגיה, סביבה, שמש, ניהול פסולת. גישה כאן.
• PlatoHealth. מודיעין ביוטכנולוגיה וניסויים קליניים. גישה כאן.
• BlockOffsets. מודרניזציה של בעלות על קיזוז סביבתי. גישה כאן.
• מקור: מודיעין נתונים של אפלטון.