Vitalik Buterin tramite il Blog di Vitalik Buterin
Questo è uno specchio del post su https://medium.com/@VitalikButerin/programmi-aritmetici-quadratici-da-zero-a-hero-f6d558cea649
Ultimamente c'è stato molto interesse per la tecnologia alla base di zk-SNARK e le persone sono in aumento cercando di demistificare qualcosa che molti chiamano “matematica lunare” a causa della sua percepita complessità indecifrabile. Gli zk-SNARK sono davvero piuttosto difficili da comprendere, soprattutto a causa dell'enorme numero di parti mobili che devono unirsi affinché il tutto funzioni, ma se analizziamo la tecnologia pezzo per pezzo, comprenderla diventa più semplice.
Lo scopo di questo post non è quello di fornire un'introduzione completa a zk-SNARKs; presuppone come conoscenza di base che (i) tu sappia cosa sono gli zk-SNARK e cosa fanno, e (ii) conosci abbastanza matematica per essere in grado di ragionare su cose come i polinomi (se l'affermazione �(�)+�(�) =(�+�)(�) , dove � e � sono polinomi, ti sembra naturale ed ovvio, allora sei al livello giusto). Piuttosto, il post scava più a fondo nei meccanismi dietro la tecnologia e cerca di spiegare nel miglior modo possibile la prima metà del gasdotto, come disegnato dal ricercatore zk-SNARK Eran Tromer qui:

I passaggi qui possono essere suddivisi in due metà. Innanzitutto, zk-SNARK non può essere applicato direttamente a nessun problema computazionale; piuttosto, devi convertire il problema nella “forma” giusta affinché il problema possa operare. La forma è chiamata “programma aritmetico quadratico” (QAP) e trasformare il codice di una funzione in uno di questi è di per sé altamente non banale. Insieme al processo per convertire il codice di una funzione in un QAP c'è un altro processo che può essere eseguito insieme in modo che se si dispone di un input per il codice è possibile creare una soluzione corrispondente (a volte chiamata "testimone" del QAP). Dopo questo, c'è un altro processo abbastanza intricato per creare l'effettiva "prova di conoscenza zero" per questo testimone, e un processo separato per verificare una prova che qualcun altro ti ha trasmesso, ma questi sono dettagli che esulano dall'ambito di questo post .
L'esempio che sceglieremo è semplice: dimostrare di conoscere la soluzione di un'equazione cubica: �3+�+5=35 (suggerimento: la risposta è 3). Questo problema è abbastanza semplice da far sì che il QAP risultante non sia così grande da intimidire, ma abbastanza non banale da poter vedere tutti i meccanismi entrare in gioco.
Scriviamo la nostra funzione nel modo seguente:
def qeval(x):
y = x**3
return x + y + 5Il semplice linguaggio di programmazione per scopi speciali che stiamo usando qui supporta l'aritmetica di base (+, -, ⋅, /), l'esponenziazione a potenza costante (�7 ma non ��) e l'assegnazione delle variabili, che è abbastanza potente da poter essere teoricamente eseguito qualsiasi calcolo al suo interno (purché il numero di passaggi di calcolo sia limitato; non sono consentiti cicli). Si noti che il modulo (%) e gli operatori di confronto (<, >, ≤, ≥) NON sono supportati, poiché non esiste un modo efficiente per eseguire il modulo o il confronto direttamente nell'aritmetica dei gruppi ciclici finiti (sii grato per questo; se ci fosse un modo per fare uno dei due, la crittografia della curva ellittica verrebbe interrotta più velocemente di quanto si possa dire "ricerca binaria" e "teorema del resto cinese").
È possibile estendere il linguaggio al modulo e ai confronti fornendo scomposizioni di bit (ad esempio 13=23+22+1) come input ausiliari, dimostrando la correttezza di tali scomposizioni ed eseguendo i calcoli nei circuiti binari; nell'aritmetica dei campi finiti, anche eseguire controlli di uguaglianza (==) è fattibile e in effetti un po' più semplice, ma questi sono entrambi dettagli di cui non entreremo adesso. Possiamo estendere il linguaggio per supportare i condizionali (es. if �<5:�=7; else: �=9) convertendoli in una forma aritmetica: �=7⋅(�<5)+9⋅(�≥5 ) tuttavia tieni presente che entrambi i "percorsi" del condizionale dovrebbero essere eseguiti e, se hai molti condizionali nidificati, ciò può portare a una grande quantità di sovraccarico.
Esaminiamo ora questo processo passo dopo passo. Se vuoi farlo tu stesso per qualsiasi pezzo di codice, I implementato un compilatore qui (solo per scopi didattici; non sono ancora pronto per creare QAP per zk-SNARK nel mondo reale!).
appiattimento
Il primo passo è una procedura di “appiattimento”, in cui convertiamo il codice originale, che può contenere istruzioni ed espressioni arbitrariamente complesse, in una sequenza di istruzioni che hanno due forme: �=� (dove � può essere una variabile o un numero ) e �=� (��) � (dove �� può essere +, −, ⋅, / e � e � possono essere variabili, numeri o loro stesse sottoespressioni). Puoi pensare a ciascuna di queste affermazioni come a una sorta di porta logica in un circuito. Il risultato del processo di appiattimento per il codice precedente è il seguente:
sym_1 = x * x
y = sym_1 * x
sym_2 = y + x
~out = sym_2 + 5Se leggi il codice originale e il codice qui, puoi vedere abbastanza facilmente che i due sono equivalenti.
Porte a R1CS
Ora lo convertiamo in qualcosa chiamato sistema di vincoli di rango 1 (R1CS). Un R1CS è una sequenza di gruppi di tre vettori (�, �, �), e la soluzione di un R1CS è un vettore �, dove � deve soddisfare l'equazione �.�⋅�.�−�.�=0, dove . rappresenta il prodotto scalare – in termini più semplici, se “uniamo insieme” � e �, moltiplicando i due valori nelle stesse posizioni, e poi prendiamo la somma di questi prodotti, poi facciamo lo stesso con � e � e poi � e � , allora il terzo risultato è uguale al prodotto dei primi due risultati. Ad esempio, questo è un R1CS soddisfatto:
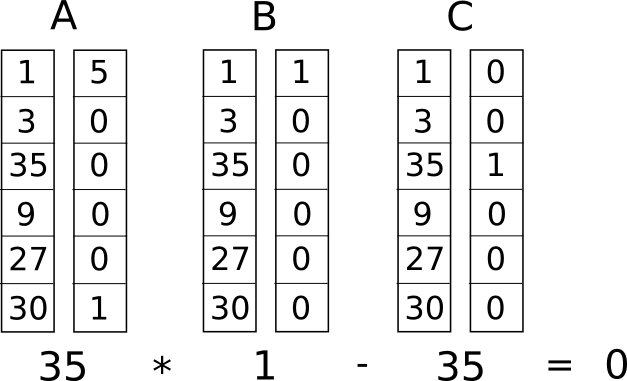
Ma invece di avere un solo vincolo, avremo molti vincoli: uno per ciascuna porta logica. Esiste un modo standard per convertire una porta logica in una tripla (�,�,�) a seconda di quale sia l'operazione (+, −, ⋅ o /) e se gli argomenti siano variabili o numeri. La lunghezza di ciascun vettore è uguale al numero totale di variabili nel sistema, inclusa una variabile dummy ~one al primo indice che rappresenta il numero 1, le variabili di input, una variabile dummy ~out che rappresenta l'output, e poi tutte le variabili variabili intermedie (����1 e ���2 sopra); i vettori saranno generalmente molto sparsi, riempiendo solo gli slot corrispondenti alle variabili che sono influenzate da qualche particolare porta logica.
Innanzitutto, forniremo la mappatura delle variabili che utilizzeremo:
'~one', 'x', '~out', 'sym_1', 'y', 'sym_2'Il vettore della soluzione sarà costituito da assegnazioni per tutte queste variabili, in questo ordine.
Ora diamo la tripla (�,�,�) per il primo cancello:
a = [0, 1, 0, 0, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 1, 0, 0]Puoi vedere che se il vettore della soluzione contiene 3 nella seconda posizione e 9 nella quarta posizione, quindi indipendentemente dal resto del contenuto del vettore della soluzione, il controllo del prodotto scalare si ridurrà a 3⋅3=9 e quindi passerà. Se il vettore soluzione ha −3 in seconda posizione e 9 in quarta posizione, anche il controllo passerà; infatti, se il vettore della soluzione ha 7 nella seconda posizione e 49 nella quarta posizione allora quel controllo passerà comunque: lo scopo di questo primo controllo è verificare la coerenza degli input e degli output solo della prima porta.
Passiamo ora al secondo cancello:
a = [0, 0, 0, 1, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 0, 1, 0]In uno stile simile al primo controllo del prodotto scalare, qui stiamo controllando che ����1⋅�=�.
Ora, la terza porta:
a = [0, 1, 0, 0, 1, 0]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 0, 0, 0, 1]Qui, lo schema è leggermente diverso: si moltiplica il primo elemento nel vettore della soluzione per il secondo elemento, quindi per il quinto elemento, sommando i due risultati e controllando se la somma è uguale al sesto elemento. Poiché il primo elemento nel vettore della soluzione è sempre uno, questo è solo un controllo di addizione, che verifica che l'output sia uguale alla somma dei due input.
Infine, la quarta porta:
a = [5, 0, 0, 0, 0, 1]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 1, 0, 0, 0]Qui stiamo valutando l'ultimo controllo, ~out =���2+5. Il controllo del prodotto scalare funziona prendendo il sesto elemento nel vettore della soluzione, aggiungendo cinque volte il primo elemento (promemoria: il primo elemento è 1, quindi questo significa effettivamente aggiungere 5) e confrontandolo con il terzo elemento, che è dove noi memorizzare la variabile di output.
Ed ecco il nostro R1CS con quattro vincoli. Il testimone è semplicemente l'assegnazione a tutte le variabili, comprese variabili di input, output e interne:
[1, 3, 35, 9, 27, 30]Puoi calcolarlo da solo semplicemente "eseguendo" il codice appiattito sopra, iniziando con l'assegnazione della variabile di input �=3 e inserendo i valori di tutte le variabili intermedie e l'output mentre le calcoli.
L'R1CS completo messo insieme è:
A
[0, 1, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 0]
[0, 1, 0, 0, 1, 0]
[5, 0, 0, 0, 0, 1]
B
[0, 1, 0, 0, 0, 0]
[0, 1, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
C
[0, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 1, 0]
[0, 0, 0, 0, 0, 1]
[0, 0, 1, 0, 0, 0]Da R1CS a QAP
Il passo successivo è prendere questo R1CS e convertirlo nel formato QAP, che implementa esattamente la stessa logica tranne l'uso di polinomi invece di prodotti scalari. Lo facciamo come segue. Si passa da quattro gruppi di tre vettori di lunghezza sei a sei gruppi di tre polinomi di grado 3, dove valutare i polinomi a ciascuno coordinata x rappresenta uno dei vincoli. Cioè, se valutiamo i polinomi a �=1, otteniamo il nostro primo insieme di vettori, se valutiamo i polinomi a �=2, otteniamo il nostro secondo insieme di vettori e così via.
Possiamo effettuare questa trasformazione utilizzando qualcosa chiamato a Interpolazione di Lagrange. Il problema che un'interpolazione di Lagrange risolve è questo: se hai un insieme di punti (cioè (�,�) coppie di coordinate), allora facendo un'interpolazione di Lagrange su quei punti ottieni un polinomio che passa attraverso tutti quei punti. Lo facciamo scomponendo il problema: per ciascuna coordinata �, creiamo un polinomio che ha la coordinata � desiderata su quella coordinata � e una coordinata � pari a 0 su tutte le altre coordinate � che ci interessano, e quindi otteniamo la coordinata finale risultato sommiamo tutti i polinomi insieme.
Facciamo un esempio. Supponiamo di volere un polinomio che passi per (1,3),(2,2) e (3,4). Iniziamo creando un polinomio che passa per (1,3), (2,0) e (3,0). In realtà, creare un polinomio che “sporga” in �=1 e sia zero negli altri punti di interesse è facile; facciamo semplicemente:
(x - 2) * (x - 3)Che assomiglia a questo:
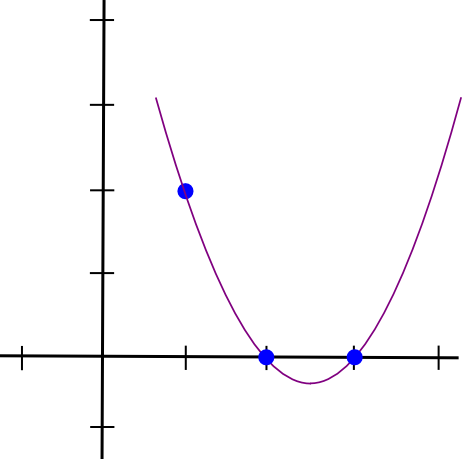
Ora dobbiamo solo “riscalarlo” in modo che l'altezza in x=1 sia corretta:
(x - 2) * (x - 3) * 3 / ((1 - 2) * (1 - 3))Questo ci dà:
1.5 * x**2 - 7.5 * x + 9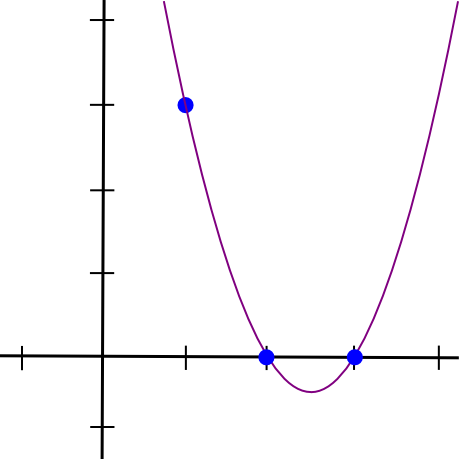
Poi facciamo lo stesso con gli altri due punti e otteniamo altri due polinomi dall'aspetto simile, tranne per il fatto che “sporgono” a �=2 e �=3 invece che �=1. Sommiamo tutti e tre insieme e otteniamo:
1.5 * x**2 - 5.5 * x + 7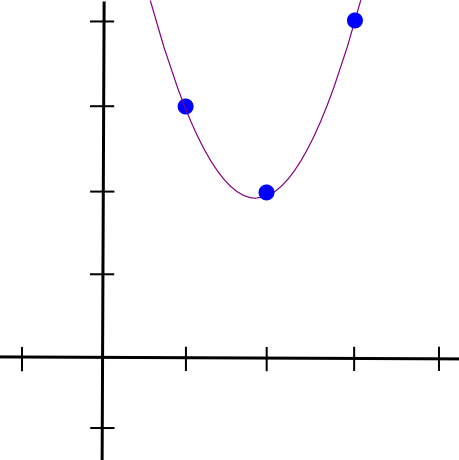
Con esattamente le coordinate che vogliamo. L'algoritmo descritto sopra richiede �(�3) tempo, poiché ci sono � punti e ogni punto richiede �(�2) tempo per moltiplicare insieme i polinomi; con un po' di riflessione, questo può essere ridotto a �(�2) tempo, e con molta più riflessione, utilizzando algoritmi di trasformata di Fourier veloci e simili, può essere ridotto ulteriormente: un'ottimizzazione cruciale quando le funzioni che vengono utilizzate in zk -Gli SNARK in pratica hanno spesso molte migliaia di porte.
Ora utilizziamo l'interpolazione di Lagrange per trasformare il nostro R1CS. Quello che faremo è prendere il primo valore da ogni vettore �, usare l'interpolazione di Lagrange per ricavarne un polinomio (dove valutando il polinomio in � si ottiene il primo valore del �esimo vettore), ripetere il processo per il primo valore di ogni vettore � e �, quindi ripetere il processo per il secondo valore, il terzo valore e così via. Per comodità riporto subito le risposte:
A polynomials
[-5.0, 9.166, -5.0, 0.833]
[8.0, -11.333, 5.0, -0.666]
[0.0, 0.0, 0.0, 0.0]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]
[-1.0, 1.833, -1.0, 0.166]
B polynomials
[3.0, -5.166, 2.5, -0.333]
[-2.0, 5.166, -2.5, 0.333]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
C polynomials
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[-1.0, 1.833, -1.0, 0.166]
[4.0, -4.333, 1.5, -0.166]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]I coefficienti sono in ordine crescente, quindi il primo polinomio sopra è in realtà 0.833⋅�3—5⋅�2+9.166⋅�−5. Questo insieme di polinomi (più un polinomio Z che spiegherò più avanti) costituisce i parametri per questa particolare istanza QAP. Tieni presente che tutto il lavoro fino a questo punto deve essere eseguito solo una volta per ogni funzione che stai tentando di utilizzare zk-SNARKs per verificare; una volta generati i parametri QAP, possono essere riutilizzati.
Proviamo a valutare tutti questi polinomi a �=1. Valutare un polinomio a �=1 significa semplicemente sommare tutti i coefficienti (come 1�=1 per tutti �), quindi non è difficile. Noi abbiamo:
A results at x=1
0
1
0
0
0
0
B results at x=1
0
1
0
0
0
0
C results at x=1
0
0
0
1
0
0Ed ecco, quello che abbiamo qui è esattamente lo stesso dell'insieme di tre vettori per la prima porta logica che abbiamo creato sopra.
Controllo del QAP
Ora qual è il punto di questa folle trasformazione? La risposta è che invece di verificare individualmente i vincoli nell'R1CS, ora possiamo verificarli tutti i vincoli contemporaneamente eseguendo il controllo del prodotto scalare sui polinomi.
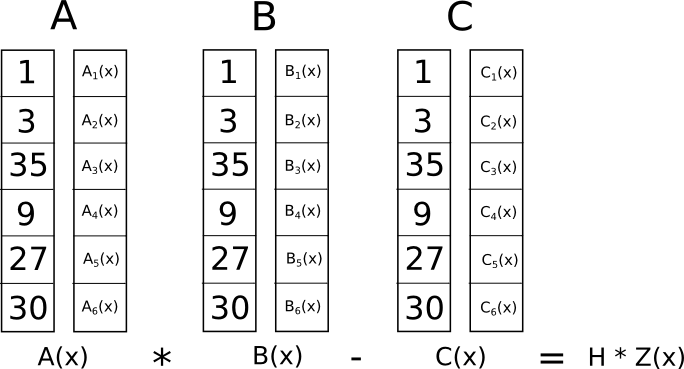
Poiché in questo caso il controllo del prodotto scalare è una serie di addizioni e moltiplicazioni di polinomi, il risultato stesso sarà un polinomio. Se il polinomio risultante, valutato ad ogni coordinata � che abbiamo usato sopra per rappresentare una porta logica, è uguale a zero, allora significa che tutti i controlli passano; se il polinomio risultante valutato in almeno una delle coordinate � che rappresentano una porta logica fornisce un valore diverso da zero, ciò significa che i valori che entrano ed escono da quella porta logica sono incoerenti (cioè la porta è �=�⋅�� �1 ma i valori forniti potrebbero essere ��=2,���1=2 e �=5).
Si noti che il polinomio risultante non deve essere di per sé zero, e in effetti nella maggior parte dei casi non lo sarà; potrebbe avere qualsiasi comportamento nei punti che non corrispondono ad alcuna porta logica, purché il risultato sia zero in tutti i punti che do corrispondere a qualche cancello. Per verificare la correttezza, in realtà non valutiamo il polinomio �=�.�⋅�.�−�.� in ogni punto corrispondente ad una porta; invece, dividiamo � per un altro polinomio, �, e controlliamo che � divida equamente � – cioè, la divisione �/� non lascia resto.
� è definito come (�−1)⋅(�−2)⋅(�−3)… – il polinomio più semplice che è uguale a zero in tutti i punti che corrispondono alle porte logiche. Questo è un fatto elementare di algebra in qualsiasi un polinomio che è uguale a zero in tutti questi punti deve essere un multiplo di questo polinomio minimo, e se un polinomio è un multiplo di � allora la sua valutazione in uno qualsiasi di questi punti sarà zero; questa equivalenza rende il nostro lavoro molto più semplice.
Ora, eseguiamo effettivamente il controllo del prodotto scalare con i polinomi sopra. Innanzitutto i polinomi intermedi:
A . s = [43.0, -73.333, 38.5, -5.166]
B . s = [-3.0, 10.333, -5.0, 0.666]
C . s = [-41.0, 71.666, -24.5, 2.833]Ora, �.�⋅�.�—�.�:
t = [-88.0, 592.666, -1063.777, 805.833, -294.777, 51.5, -3.444]Ora, il polinomio minimo �=(�−1)⋅(�−2)⋅(�−3)⋅(�−4):
Z = [24, -50, 35, -10, 1]E se dividiamo il risultato sopra per �, otteniamo:
h = t / Z = [-3.666, 17.055, -3.444]Senza resto.
E così abbiamo la soluzione per il QAP. Se proviamo a falsificare una qualsiasi delle variabili nella soluzione R1CS da cui stiamo derivando questa soluzione QAP - diciamo, impostiamo l'ultima a 31 invece che a 30, allora otteniamo un polinomio � che fallisce uno dei controlli (in quel particolare caso, il risultato a �=3 sarebbe uguale a −1 invece di 0), e inoltre � non sarebbe un multiplo di �; piuttosto, dividendo �/� si otterrebbe un resto di [−5.0,8.833,−4.5,0.666].
Si noti che quanto sopra è una semplificazione; “nel mondo reale”, l’addizione, la moltiplicazione, la sottrazione e la divisione non avverranno con numeri regolari, ma piuttosto con elementi di campi finiti – un tipo spettrale di aritmetica che è auto-coerente, quindi tutte le leggi algebriche che conosciamo e amiamo ancora sono vere, ma dove tutte le risposte sono elementi di un insieme di dimensione finita, solitamente numeri interi compresi tra 0 e �−1 per alcuni �. Ad esempio, se �=13, allora 1/2=7 (e 7⋅2=1),3⋅5=2 e così via. L'uso dell'aritmetica dei campi finiti elimina la necessità di preoccuparsi degli errori di arrotondamento e consente al sistema di funzionare bene con le curve ellittiche, che finiscono per essere necessarie per il resto del meccanismo zk-SNARK che rende il protocollo zk-SNARK effettivamente sicuro.
Un ringraziamento speciale a Eran Tromer per avermi aiutato a spiegarmi molti dettagli sul funzionamento interno di zk-SNARKs.
- Distribuzione di contenuti basati su SEO e PR. Ricevi amplificazione oggi.
- PlatoData.Network Generativo verticale Ai. Potenzia te stesso. Accedi qui.
- PlatoAiStream. Intelligenza Web3. Conoscenza amplificata. Accedi qui.
- PlatoneESG. Carbonio, Tecnologia pulita, Energia, Ambiente, Solare, Gestione dei rifiuti. Accedi qui.
- Platone Salute. Intelligence sulle biotecnologie e sulle sperimentazioni cliniche. Accedi qui.
- BlockOffset. Modernizzare la proprietà della compensazione ambientale. Accedi qui.
- Fonte: Platone Data Intelligence.
