Distance quantique de Wasserstein basée sur une optimisation sur des états séparables

Distance quantique de Wasserstein basée sur une optimisation sur des états séparables

Horodatage: 16 octobre 2023 10h35
Nœud source: 2938953

Géza Toth1,2,3,4,5 et József Pitrik5,6,7

1Physique Théorique, Université du Pays Basque UPV/EHU, ES-48080 Bilbao, Espagne
2EHU Quantum Center, Université du Pays Basque UPV/EHU, Barrio Sarriena s/n, ES-48940 Leioa, Biscaye, Espagne
3Donostia International Physics Center (DIPC), ES-20080 San Sebastián, Espagne
4IKERBASQUE, Fondation basque pour la science, ES-48011 Bilbao, Espagne
5Institut de physique et d'optique du solide, Centre de recherche Wigner pour la physique, HU-1525 Budapest, Hongrie
6Institut de mathématiques Alfréd Rényi, Reáltanoda u. 13-15., HU-1053 Budapest, Hongrie
7Département d'analyse et de recherche opérationnelle, Institut de mathématiques, Université de technologie et d'économie de Budapest, Müegyetem rkp. 3., HU-1111 Budapest, Hongrie

Vous trouvez cet article intéressant ou souhaitez en discuter? Scite ou laisse un commentaire sur SciRate.

Abstract

Nous définissons la distance quantique de Wasserstein de telle sorte que l'optimisation du couplage soit effectuée sur des états séparables bipartites plutôt que sur des états quantiques bipartites en général, et examinons ses propriétés. Étonnamment, nous constatons que la distance de soi est liée à l’information quantique de Fisher. Nous présentons une carte de transport correspondant à un état séparable bipartite optimal. Nous discutons de la façon dont la distance quantique de Wasserstein introduite est connectée aux critères de détection de l'intrication quantique. Nous définissons des quantités de type variance qui peuvent être obtenues à partir de la distance quantique de Wasserstein en remplaçant la minimisation sur les états quantiques par une maximisation. Nous étendons nos résultats à une famille de quantités d'informations quantiques généralisées de Fisher.

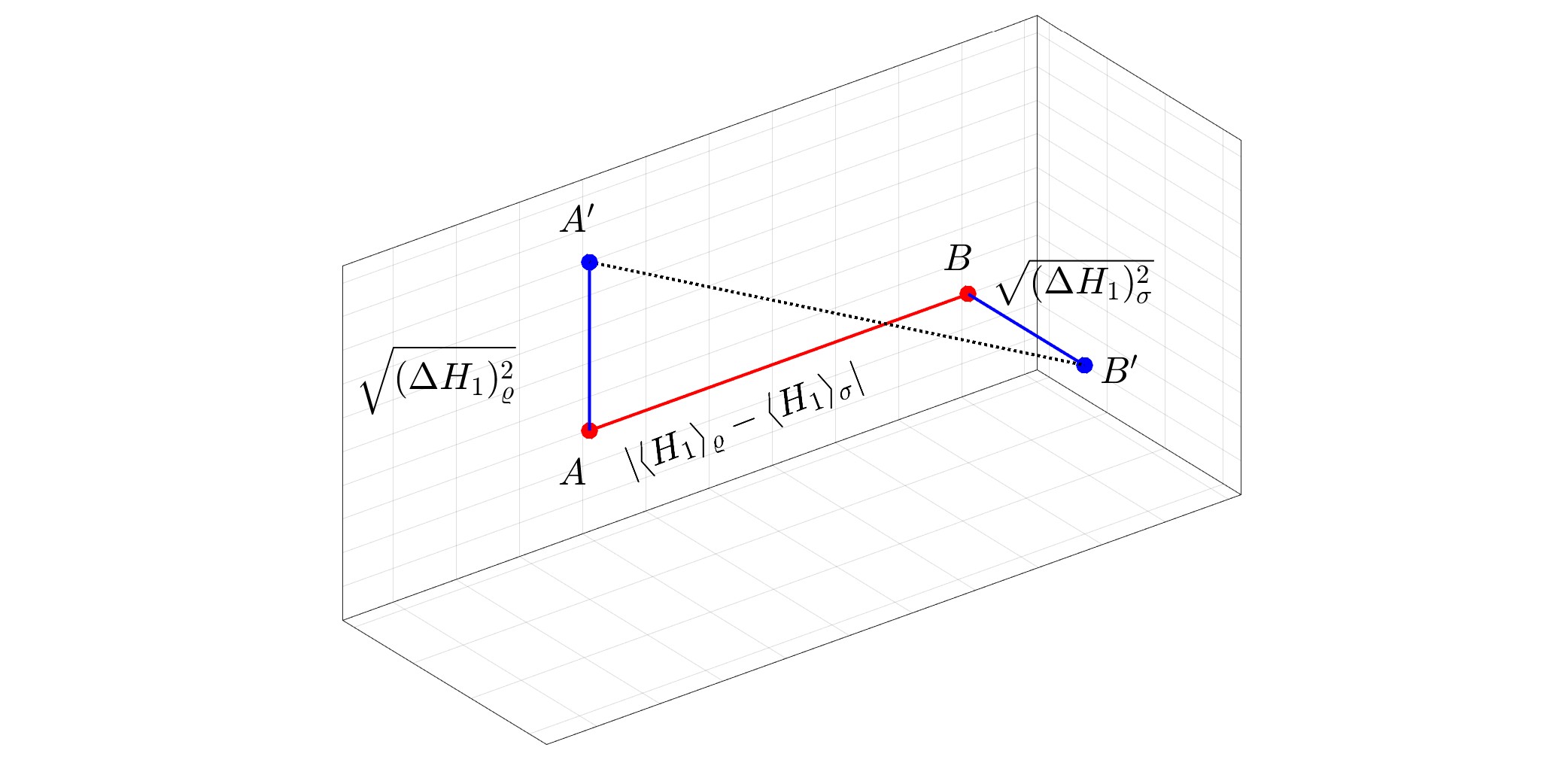
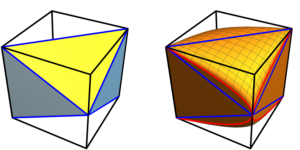
Image présentée : Représentation géométrique de la distance quantique de Wasserstein entre un état pur $varrho$ et un état mixte $sigma$ pour $N=1.$ La distance quantique de Wasserstein est égale à $1/sqrt2$ fois la distance euclidienne habituelle entre $A'$ et $B'.$

Résumé populaire

Dans la vie de tous les jours, la distance entre deux villes nous indique combien de kilomètres nous devons parcourir pour passer de l'une à l'autre. Il est également possible de caractériser la facilité avec laquelle nous pouvons nous rendre d'une ville à l'autre en mesurant la consommation de carburant au cours de notre trajet. Cette dernière est plus informative dans le sens où elle reflète le coût du déplacement lié à la topographie de la route, c'est-à-dire qu'elle est sensible à la métrique sous-jacente. Imaginons ensuite que nous devions déplacer un tas de sable d’un endroit à un autre et que le nouveau tas puisse avoir une forme différente. Dans ce cas encore, on peut caractériser l’effort de déplacement du sable par le coût du transport.

Les distances jouent un rôle central en mathématiques, en physique et en ingénierie. Un problème fondamental en probabilités et en statistiques est de trouver des mesures utiles de la distance entre deux distributions de probabilité. Malheureusement, de nombreuses notions de distance entre les distributions de probabilité, disons p(x) et q(x), sont maximales si elles ne se chevauchent pas, c'est-à-dire que l'une est toujours nulle lorsque l'autre est non nulle. Ceci n’est pas pratique pour de nombreuses applications. Par exemple, pour revenir à l’analogie avec le sable, deux tas de sable qui ne se chevauchent pas semblent être à égale distance l’un de l’autre, que leur distance soit de 10 km ou de 100 km. La théorie du transport optimal est un moyen de construire une notion alternative de distance entre les distributions de probabilité, appelée distance de Wasserstein. Il peut être non maximal même si les distributions ne se chevauchent pas, il est sensible à la métrique sous-jacente (c'est-à-dire le coût du transport), et essentiellement, il exprime l'effort que nous devons faire pour passer de l'une à l'autre. comme s'il s'agissait de collines de sable.

Récemment, la distance quantique de Wasserstein a été définie en généralisant la distance classique de Wasserstein. Elle est basée sur la minimisation d'une fonction de coût sur les états quantiques d'un système quantique bipartite. Il possède une propriété analogue à celle mentionnée ci-dessus dans le monde quantique. Cela peut être non maximal pour les états orthogonaux, ce qui est utile, par exemple, lorsque nous devons enseigner des données quantiques à un algorithme.

Comme on peut s’y attendre, la distance quantique de Wasserstein possède également des propriétés très différentes de celles de son homologue classique. Par exemple, lorsque nous mesurons la distance d’un état quantique à lui-même, elle peut être différente de zéro. Bien que cela soit déjà déroutant, il a également été découvert que la distance de soi est liée à l'information asymétrique de Wigner-Yanase, introduite en 1963 par le lauréat du prix Nobel EP Wigner, qui a apporté une contribution vitale aux fondements de la physique quantique et de MM Yanase.

Dans notre article, nous examinons cette découverte mystérieuse sous un autre angle. Nous limitons la minimisation mentionnée ci-dessus aux états dits séparables. Ce sont les états quantiques qui ne contiennent pas d’intrication. Nous constatons que la distance de soi devient l’information quantique de Fisher, une quantité centrale en métrologie quantique et en théorie de l’estimation quantique, et apparaissant par exemple dans la célèbre liaison de Cramer-Rao. En examinant les propriétés d’une telle distance de Wasserstein, nos travaux ouvrent la voie à la connexion de la théorie de la distance quantique de Wasserstein à la théorie de l’intrication quantique.

► Données BibTeX

► Références

G.Monge. « Mémoire sur la théorie des déblais et des remblais ». Mémoires de l'Académie Royale des Sciences de Paris (1781).

L. Kantorovitch. « Sur la translocation des masses ». Sciences de gestion 5, 1–4 (1958). URL : http://​/​www.jstor.org/​stable/​2626967.
http: / / www.jstor.org/ stable / 2626967

Emmanuel Boissard, Thibaut Le Gouic et Jean-Michel Loubes. « Estimation du modèle de distribution avec les métriques Wasserstein ». Bernoulli 21, 740-759 (2015).
https://​/​doi.org/​10.3150/​13-bej585

Oleg Butkovski. "Taux sous-géométriques de convergence des processus de Markov dans la métrique de Wasserstein". Anne. Appl. Probablement. 24, 526-552 (2014).
https://​/​doi.org/​10.1214/​13-AAP922

M. Hairer, J.-C. Mattingly et M. Scheutzow. "Couplage asymptotique et forme générale du théorème de Harris avec applications aux équations de retard stochastique". Probablement. Théorie Relat. Champs 149, 223-259 (2011).
https:/​/​doi.org/​10.1007/​s00440-009-0250-6

M. Hairer et JC Mattingly. "Écarts spectraux dans les distances de Wasserstein et les équations stochastiques de Navier-Stokes 2D". Anne. Probablement. 36, 2050-2091 (2008).
https://​/​doi.org/​10.1214/​08-AOP392

A. Figalli, F. Maggi et A. Pratelli. « Une approche des transports collectifs aux inégalités isopérimétriques quantitatives ». Inventer. Mathématiques. 182, 167-211. (2010).
https: / / doi.org/ 10.1007 / s00222-010-0261-z

A. Figalli et F. Maggi. « Sur la forme des gouttes et des cristaux liquides dans le régime des petites masses ». Cambre. Ration. Mécanique. Anal. 201, 143-207 (2011).
https: / / doi.org/ 10.1007 / s00205-010-0383-x

J. Lott et C. Villani. "Courbure de Ricci pour les espaces de mesure métrique via un transport optimal". Anne. des mathématiques. 169 (3), 903-991 (2009).
https://​/​doi.org/​10.48550/​arXiv.math/​0412127

Max-K. von Renesse et Karl-Theodor Sturm. "Inégalités de transport, estimations de gradient, entropie et courbure de Ricci". Comm. Application pure. Mathématiques. 58, 923-940 (2005).
https: / / doi.org/ 10.1002 / cpa.20060

Karl-Theodor Sturm. « Sur la géométrie des espaces de mesure métriques I ». Acta Math. 196, 65-131 (2006).
https:/​/​doi.org/​10.1007/​s11511-006-0002-8

Karl-Theodor Sturm. « Sur la géométrie des espaces de mesure métrique II ». Acta Math. 196, 133-177 (2006).
https:/​/​doi.org/​10.1007/​s11511-006-0003-7

Benoît Kloeckner. « Une étude géométrique des espaces de Wasserstein : les espaces euclidiens ». Annali della Scuola Normale Superiore di Pisa – Classe di Science, Scuola Normale Superiore 2010 IX (2), 297-323 (2010).
https: / / doi.org/ 10.2422 / 2036-2145.2010.2.03

György Pál Gehér, Tamás Titkos et Dániel Virosztek. « Sur les plongements isométriques des espaces de Wasserstein – le cas discret ». J. Math. Anal. Appl. 480, 123435 (2019).
https://​/​doi.org/​10.1016/​j.jmaa.2019.123435

György Pál Gehér, T. Titkos, Dániel Virosztek. "Etude isométrique des espaces de Wasserstein – la vraie ligne". Trans. Amer. Mathématiques. Soc. 373, 5855-5883 (2020).
https://​/​doi.org/​10.1090/​tran/​8113

György Pál Gehér, Tamás Titkos et Dániel Virosztek. « Le groupe d'isométrie des espaces de Wasserstein : le cas hilbertien ». J. Londres. Mathématiques. Soc. 106, 3865-3894 (2022).
https://​/​doi.org/​10.1112/​jlms.12676

György Pál Gehér, Tamás Titkos et Dániel Virosztek. « Rigidité isométrique des tores et sphères de Wasserstein ». Mathématika 69, 20-32 (2023).
https://​/​doi.org/​10.1112/​mtk.12174

Gergely Kiss et Tamás Titkos. « Rigidité isométrique des espaces de Wasserstein : le cas graphique métrique ». Proc. Suis. Mathématiques. Soc. 150, 4083-4097 (2022).
https://​/​doi.org/​10.1090/​proc/​15977

György Pál Gehér, Tamás Titkos et Dániel Virosztek. "Sur le flux isométrique exotique de l'espace quadratique de Wasserstein sur la ligne réelle". Application d'algèbre linéaire. (2023).
https: / / doi.org/ 10.1016 / j.laa.2023.02.016

S. Kolouri, SR Park et GK Rohde. "La transformation de distribution cumulative du Radon et son application à la classification d'images". IEEETrans. Processus d'images. 25, 920-934 (2016).
https://​/​doi.org/​10.1109/​TIP.2015.2509419

W. Wang, D. Slepc̆ev, S. Basu, JA Ozolek et GK Rohde. "Un cadre de transport optimal linéaire pour quantifier et visualiser les variations dans des ensembles d'images". Int. J. Informatique. Vis. 101, 254-269 (2013).
https: / / doi.org/ 10.1007 / s11263-012-0566-z

S. Kolouri, S. Park, M. Thorpe, D. Slepc̆ev, GK Rohde. « Transport de masse optimal : applications de traitement du signal et d'apprentissage automatique ». Magazine de traitement du signal IEEE 34, 43-59 (2017).
https: / / doi.org/ 10.1109 / MSP.2017.2695801

A. Gramfort, G. Peyré et M. Cuturi. « Moyenne de transport rapide et optimale des données de neuroimagerie ». Traitement de l'information en imagerie médicale. IPMI 2015. Notes de cours en informatique 9123, 261-272 (2015).
https:/​/​doi.org/​10.1007/​978-3-319-19992-4_20

Z. Su, W. Zeng, Y. Wang, ZL Lu et X. Gu. "Classification des formes utilisant la distance de Wasserstein pour l'analyse de la morphométrie cérébrale". Traitement de l'information en imagerie médicale. IPMI 2015. Notes de cours en informatique 24, 411-423 (2015).
https:/​/​doi.org/​10.1007/​978-3-319-19992-4_32

Martin Arjovsky, Soumith Chintala et Léon Bottou. «Réseaux contradictoires génératifs de Wasserstein». Dans Doina Precup et Yee Whye Teh, éditeurs, Actes de la 34e Conférence internationale sur l'apprentissage automatique. Volume 70 des Actes de recherche sur l'apprentissage automatique, pages 214-223. PMLR (2017). arXiv :1701.07875.
arXiv: 1701.07875

TA El Moselhy et YM Marzouk. "Inférence bayésienne avec cartes optimales". J. Informatique. Phys. 231, 7815-7850 (2012).
https: / / doi.org/ 10.1016 / j.jcp.2012.07.022

Gabriel Peyré et Marco Cuturi. « Transport informatique optimal : avec des applications à la science des données ». Trouvé. Apprentissage automatique des tendances. 11, 355-602 (2019).
https: / / doi.org/ 10.1561 / 2200000073

Charlie Frogner, Chiyuan Zhang, Hossein Mobahi, Mauricio Araya et Tomaso A Poggio. « Apprendre avec une perte de Wasserstein ». Dans C. Cortes, N. Lawrence, D. Lee, M. Sugiyama et R. Garnett, éditeurs, Advances in Neural Information Processing Systems. Volume 28. Curran Associates, Inc. (2015). arXiv : 1506.05439.
arXiv: 1506.05439

A. Ramdas, NG Trillos et M. Cuturi. "Sur les tests à deux échantillons de Wasserstein et les familles associées de tests non paramétriques". Entropie 19, 47. (2017).
https: / / doi.org/ 10.3390 / e19020047

S. Srivastava, C. Li et DB Dunson. "Bayes évolutif via Barycenter dans l'espace Wasserstein". J. Mach. Apprendre. Rés. 19, 1–35 (2018). arXiv : 1508.05880.
arXiv: 1508.05880

Karol Życzkowski et Wojeciech Slomczynski. "La distance de Monge entre les états quantiques". J. Phys. R : Mathématiques. Gen.31, 9095-9104 (1998).
https:/​/​doi.org/​10.1088/​0305-4470/​31/​45/​009

Karol Życzkowski et Wojciech Slomczynski. « La métrique Monge sur la sphère et la géométrie des états quantiques ». J. Phys. R : Mathématiques. Gen.34, 6689-6722 (2001).
https:/​/​doi.org/​10.1088/​0305-4470/​34/​34/​311

Ingemar Bengtsson et Karol Życzkowski. "Géométrie des états quantiques: Une introduction à l'intrication quantique". La presse de l'Universite de Cambridge. (2006).
https: / / doi.org/ 10.1017 / CBO9780511535048

P. Biane et D. Voiculescu. "Un analogue de probabilité libre de la métrique de Wasserstein sur l'espace d'état de trace". GAFA, Géom. Fonction. Anal. 11, 1125-1138 (2001).
https:/​/​doi.org/​10.1007/​s00039-001-8226-4

Eric A. Carlen et Jan Maas. "Un analogue de la métrique 2-Wasserstein en probabilité non commutative sous laquelle l'équation fermionique de Fokker-Planck est un flux de gradient pour l'entropie". Commun. Mathématiques. Phys. 331, 887-926 (2014).
https:/​/​doi.org/​10.1007/​s00220-014-2124-8

Eric A. Carlen et Jan Maas. "Flux de gradient et inégalités d'entropie pour les semi-groupes quantiques de Markov avec équilibre détaillé". J. Fonction. Anal. 273, 1810-1869 (2017).
https: / / doi.org/ 10.1016 / j.jfa.2017.05.003

Eric A. Carlen et Jan Maas. « Calcul non commutatif, transport optimal et inégalités fonctionnelles dans les systèmes quantiques dissipatifs ». J.Stat. Phys. 178, 319-378 (2020).
https: / / doi.org/ 10.1007 / s10955-019-02434-w

Nilanjana Datta et Cambyse Rouzé. "Concentration d'états quantiques à partir des inégalités de fonctionnalité quantique et de coût de transport". J. Math. Phys. 60, 012202 (2019).
https: / / doi.org/ 10.1063 / 1.5023210

Nilanjana Datta et Cambyse Rouzé. « Relier l'entropie relative, le transport optimal et les informations de Fisher : une inégalité quantique HWI ». Anne. Henri Poincaré 21, 2115-2150 (2020).
https:/​/​doi.org/​10.1007/​s00023-020-00891-8

François Golse, Clément Mouhot et Thierry Paul. « Sur le champ moyen et les limites classiques de la mécanique quantique ». Commun. Mathématiques. Phys. 343, 165-205 (2016).
https:/​/​doi.org/​10.1007/​s00220-015-2485-7

François Golse et Thierry Paul. "L'équation de Schrödinger en champ moyen et régime semi-classique". Cambre. Ration. Mécanique. Anal. 223, 57-94 (2017).
https: / / doi.org/ 10.1007 / s00205-016-1031-x

François Golse et Thierry Paul. "Les paquets d'ondes et la distance quadratique de Monge-Kantorovitch en mécanique quantique". Comptes Rendus Math. 356, 177-197 (2018).
https://​/​doi.org/​10.1016/​j.crma.2017.12.007

François Golse. "Le problème quantique du corps $N$ dans le régime de champ moyen et semi-classique". Phil. Trans. R. Soc. A 376, 20170229 (2018).
https: / / doi.org/ 10.1098 / rsta.2017.0229

E. Caglioti, F. Golse et T. Paul. « Le transport quantique optimal est moins cher ». J.Stat. Phys. 181, 149-162 (2020).
https:/​/​doi.org/​10.1007/​s10955-020-02571-7

Emanuele Caglioti, François Golse et Thierry Paul. « Vers un transport optimal pour les densités quantiques ». arXiv :2101.03256 (2021).
https://​/​doi.org/​10.48550/​arXiv.2101.03256
arXiv: 2101.03256

Giacomo De Palma et Dario Trevisan. « Transport quantique optimal avec canaux quantiques ». Anne. Henri Poincaré 22, 3199-3234 (2021).
https:/​/​doi.org/​10.1007/​s00023-021-01042-3

Giacomo De Palma, Milad Marvian, Dario Trevisan et Seth Lloyd. "La distance quantique de Wasserstein d'ordre 1". IEEETrans. Inf. Théorie 67, 6627-6643 (2021).
https: / / doi.org/ 10.1109 / TIT.2021.3076442

Shmuel Friedland, Michał Eckstein, Sam Cole et Karol Życzkowski. "Problème quantique de Monge-Kantorovich et distance de transport entre les matrices de densité". Phys. Le révérend Lett. 129, 110402 (2022).
https: / / doi.org/ 10.1103 / PhysRevLett.129.110402

Sam Cole, Michał Eckstein, Shmuel Friedland et Karol Życzkowski. « Transport quantique optimal ». arXiv :2105.06922 (2021).
https://​/​doi.org/​10.48550/​arXiv.2105.06922
arXiv: 2105.06922

R. Bistroń, M. Eckstein et K. Życzkowski. « Monotonie d'une distance quantique 2-Wasserstein ». J. Phys. R : Mathématiques. Théorique. 56, 095301 (2023).
https:/​/​doi.org/​10.1088/​1751-8121/​acb9c8

György Pál Gehér, József Pitrik, Tamás Titkos et Dániel Virosztek. "Isométries quantiques de Wasserstein sur l'espace d'état des qubits". J. Math. Anal. Appl. 522, 126955 (2023).
https://​/​doi.org/​10.1016/​j.jmaa.2022.126955

Lu Li, Kaifeng Bu, Dax Enshan Koh, Arthur Jaffe et Seth Lloyd. « Complexité de Wasserstein des circuits quantiques ». arXiv : 2208.06306 (2022).
https://​/​doi.org/​10.48550/​arXiv.2208.06306

Bobak Toussi Kiani, Giacomo De Palma, Milad Marvian, Zi-Wen Liu et Seth Lloyd. "Apprentissage des données quantiques avec la distance du terrassement quantique". Science quantique. Technologie. 7, 045002 (2022).
https:/​/​doi.org/​10.1088/​2058-9565/​ac79c9

EP Wigner et Mutsuo M. Yanase. « Contenu informatif des distributions ». Proc. Natl. Acad. Sci. États-Unis 49, 910-918 (1963).
https: / / doi.org/ 10.1073 / pnas.49.6.910

Ryszard Horodecki, Paweł Horodecki, Michał Horodecki et Karol Horodecki. "Intrication quantique". Rév. Mod. Phys. 81, 865–942 (2009).
https: / / doi.org/ 10.1103 / RevModPhys.81.865

Otfried Gühne et Géza Tóth. "Détection d'enchevêtrement". Phys. Rep. 474, 1–75 (2009).
https: / / doi.org/ 10.1016 / j.physrep.2009.02.004

Nicolai Friis, Giuseppe Vitagliano, Mehul Malik et Marcus Huber. "Certification d'intrication de la théorie à l'expérience". Nat. Rév. Phys. 1, 72–87 (2019).
https:/​/​doi.org/​10.1038/​s42254-018-0003-5

Vittorio Giovannetti, Seth Lloyd et Lorenzo Maccone. "Mesures améliorées quantiques : battre la limite quantique standard". Sciences 306, 1330-1336 (2004).
https: / / doi.org/ 10.1126 / science.1104149

Matteo GA Paris. « Estimation quantique pour la technologie quantique ». Int. J. Quant. Inf. 07, 125-137 (2009).
https: / / doi.org/ 10.1142 / S0219749909004839

Rafal Demkowicz-Dobrzanski, Marcin Jarzyna et Jan Kolodynski. « Chapitre quatre – Limites quantiques en interférométrie optique ». Programme. Optique 60, 345 – 435 (2015). arXiv : 1405.7703.
https: / / doi.org/ 10.1016 / bs.po.2015.02.003
arXiv: 1405.7703

Luca Pezze et Augusto Smerzi. "Théorie quantique de l'estimation de phase". Dans GM Tino et MA Kasevich, éditeurs, Atom Interferometry (Proc. Int. School of Physics 'Enrico Fermi', Cours 188, Varenna). Pages 691 à 741. IOS Press, Amsterdam (2014). arXiv : 1411.5164.
arXiv: 1411.5164

Géza Tóth et Dénes Petz. "Propriétés extrêmes de la variance et information quantique de Fisher". Phys. Rév.A 87, 032324 (2013).
https: / / doi.org/ 10.1103 / PhysRevA.87.032324

Sixia Yu. "L'information quantique de Fisher comme toit convexe de la variance". arXiv : 1302.5311 (2013).
https://​/​doi.org/​10.48550/​arXiv.1302.5311
arXiv: 1302.5311

Géza Tóth et Florian Fröwis. « Relations d'incertitude avec la variance et l'information quantique de Fisher basées sur des décompositions convexes de matrices de densité ». Phys. Rév.Recherche 4, 013075 (2022).
https: / / doi.org/ 10.1103 / PhysRevResearch.4.013075

Shao-Hen Chiew et Manuel Gessner. "Amélioration des relations d'incertitude de somme avec les informations quantiques de Fisher". Phys. Rév.Recherche 4, 013076 (2022).
https: / / doi.org/ 10.1103 / PhysRevResearch.4.013076

CW Helstrom. « Théorie de la détection et de l'estimation quantique ». Presse académique, New York. (1976). URL : www.elsevier.com/​books/​quantum-detection-and-estimation-theory/​helstrom/​978-0-12-340050-5.
https:/​/​www.elsevier.com/​books/​quantum-detection-and-estimation-theory/​helstrom/​978-0-12-340050-5

AS Holevo. « Aspects probabilistes et statistiques de la théorie quantique ». Hollande du Nord, Amsterdam. (1982).

Samuel L. Braunstein et Carlton M. Caves. "Distance statistique et géométrie des états quantiques". Phys. Rév. Lett. 72, 3439–3443 (1994).
https: / / doi.org/ 10.1103 / PhysRevLett.72.3439

Samuel L Braunstein, Carlton M Caves et Gerard J Milburn. « Relations d'incertitude généralisées : théorie, exemples et invariance de Lorentz ». Anne. Phys. 247, 135-173 (1996).
https: / / doi.org/ 10.1006 / aphy.1996.0040

Dénes Petz. "Théorie de l'information quantique et statistiques quantiques". Springer, Berlin, Heilderberg. (2008).
https:/​/​doi.org/​10.1007/​978-3-540-74636-2

Géza Toth et Iagoba Apellaniz. « La métrologie quantique du point de vue de la science de l'information quantique ». J.Phys. R : Mathématiques. Théor. 47, 424006 (2014).
https:/​/​doi.org/​10.1088/​1751-8113/​47/​42/​424006

Luca Pezzè, Augusto Smerzi, Markus K. Oberthaler, Roman Schmied et Philipp Treutlein. « Métrologie quantique avec états non classiques d'ensembles atomiques ». Rév. Mod. Phys. 90, 035005 (2018).
https: / / doi.org/ 10.1103 / RevModPhys.90.035005

Marco Barbieri. « Métrologie quantique optique ». PRX Quantique 3, 010202 (2022).
https: / / doi.org/ 10.1103 / PRXQuantum.3.010202

Zoltán Léka et Dénes Petz. "Quelques décompositions de variances matricielles". Probablement. Mathématiques. Statiste. 33, 191-199 (2013). arXiv : 1408.2707.
arXiv: 1408.2707

Dénes Petz et Dániel Virosztek. "Un théorème de caractérisation des variances matricielles". Acta Sci. Mathématiques. (Szeged) 80, 681-687 (2014).
https://​/​doi.org/​10.14232/​actasm-013-789-z

Akio Fujiwara et Hiroshi Imai. "Un faisceau de fibres sur des variétés de canaux quantiques et son application aux statistiques quantiques". J. Phys. R : Mathématiques. Théorique. 41, 255304 (2008).
https:/​/​doi.org/​10.1088/​1751-8113/​41/​25/​255304

BM Escher, RL de Matos Filho et L. Davidovitch. "Cadre général pour l'estimation de la limite ultime de précision en métrologie quantique bruyante". Nat. Phys. 7, 406-411 (2011).
https: / / doi.org/ 10.1038 / nphys1958

Rafał Demkowicz-Dobrzański, Jan Kołodyński et Mădălin Guţă. « La limite insaisissable de Heisenberg dans la métrologie quantique améliorée ». Nat. Commun. 3, 1063 (2012).
https: / / doi.org/ 10.1038 / ncomms2067

Iman Marvien. "Interprétation opérationnelle des informations des pêcheurs quantiques en thermodynamique quantique". Phys. Le révérend Lett. 129, 190502 (2022).
https: / / doi.org/ 10.1103 / PhysRevLett.129.190502

Reinhard F. Werner. "États quantiques avec corrélations d'Einstein-Podolsky-Rosen admettant un modèle à variables cachées". Phys. Rév.A 40, 4277-4281 (1989).
https: / / doi.org/ 10.1103 / PhysRevA.40.4277

K. Eckert, J. Schliemann, D. Bruss et M. Lewenstein. "Corrélations quantiques dans les systèmes de particules indiscernables". Anne. Phys. 299, 88-127 (2002).
https: / / doi.org/ 10.1006 / aphy.2002.6268

Tsubasa Ichikawa, Toshihiko Sasaki, Izumi Tsutsui et Nobuhiro Yonezawa. «Symétrie d'échange et intrication multipartite». Phys. Rév.A 78, 052105 (2008).
https: / / doi.org/ 10.1103 / PhysRevA.78.052105

Pawel Horodecki. « Critère de séparabilité et états mixtes inséparables à transposition partielle positive ». Phys. Lett. A 232, 333-339 (1997).
https:/​/​doi.org/​10.1016/​S0375-9601(97)00416-7

Asher Pérès. "Critère de séparabilité pour les matrices de densité". Phys. Rév. Lett. 77, 1413-1415 (1996).
https: / / doi.org/ 10.1103 / PhysRevLett.77.1413

Paweł Horodecki, Michał Horodecki et Ryszard Horodecki. "L'enchevêtrement lié peut être activé". Phys. Le révérend Lett. 82, 1056-1059 (1999).
https: / / doi.org/ 10.1103 / PhysRevLett.82.1056

Géza Tóth et Tamás Vértesi. « Les états quantiques avec une transposition partielle positive sont utiles pour la métrologie ». Phys. Le révérend Lett. 120, 020506 (2018).
https: / / doi.org/ 10.1103 / PhysRevLett.120.020506

Scott Hill et William K. Wootters. "Intrication d'une paire de bits quantiques". Phys. Le révérend Lett. 78, 5022-5025 (1997).
https: / / doi.org/ 10.1103 / PhysRevLett.78.5022

William K. Wootters. "Enchevêtrement de formation d'un état arbitraire de deux qubits". Phys. Rév. Lett. 80, 2245-2248 (1998).
https: / / doi.org/ 10.1103 / PhysRevLett.80.2245

David P. DiVincenzo, Christopher A. Fuchs, Hideo Mabuchi, John A. Smolin, Ashish Thapliyal et Armin Uhlmann. «Enchevêtrement d'assistance». quant-ph/​9803033 (1998).
https://​/​doi.org/​10.48550/​arXiv.quant-ph/​9803033
arXiv: quant-ph / 9803033

John A. Smolin, Frank Verstraete et Andreas Winter. « Enchevêtrement de l’assistance et distillation étatique multipartite ». Phys. Rév.A 72, 052317 (2005).
https: / / doi.org/ 10.1103 / PhysRevA.72.052317

Holger F. Hofmann et Shigeki Takeuchi. "La violation des relations d'incertitude locales comme signature de l'intrication". Phys. Rév.A 68, 032103 (2003).
https: / / doi.org/ 10.1103 / PhysRevA.68.032103

Otfried Gühne. "Caractériser l'intrication via des relations d'incertitude". Phys. Le révérend Lett. 92, 117903 (2004).
https: / / doi.org/ 10.1103 / PhysRevLett.92.117903

Otfried Gühne, Mátyás Mechler, Géza Tóth et Peter Adam. "Les critères d'intrication basés sur des relations d'incertitude locales sont strictement plus forts que le critère calculable de normes croisées". Phys. Rév.A 74, 010301 (2006).
https: / / doi.org/ 10.1103 / PhysRevA.74.010301

Giuseppe Vitagliano, Philipp Hyllus, Iñigo L. Egusquiza et Géza Tóth. "Inégalités de compression de spin pour un spin arbitraire". Phys. Rév. Lett. 107, 240502 (2011).
https: / / doi.org/ 10.1103 / PhysRevLett.107.240502

AR Edmonds. « Moment angulaire en mécanique quantique ». Presse de l'Université de Princeton. (1957).
https: / / doi.org/ 10.1515 / 9781400884186

Géza Toth. "Détection d'intrication dans les réseaux optiques d'atomes bosoniques avec mesures collectives". Phys. Rev. A 69, 052327 (2004).
https: / / doi.org/ 10.1103 / PhysRevA.69.052327

Géza Tóth, Christian Knapp, Otfried Gühne et Hans J. Briegel. "Les inégalités de compression de spin optimales détectent l'intrication liée dans les modèles de spin". Phys. Rév. Lett. 99, 250405 (2007).
https: / / doi.org/ 10.1103 / PhysRevLett.99.250405

Géza Tóth et Morgan W Mitchell. "Génération d'états singules macroscopiques dans des ensembles atomiques". Nouveau J. Phys. 12, 053007 (2010).
https:/​/​doi.org/​10.1088/​1367-2630/​12/​5/​053007

Géza Toth. "Détection de l'intrication multipartite au voisinage des états de Dicke symétriques". J. Opt. Soc. Suis. B24, 275-282 (2007).
https: / / doi.org/ 10.1364 / JOSAB.24.000275

Géza Tóth, Tobias Moroder et Otfried Gühne. « Évaluer les mesures d'enchevêtrement des toits convexes ». Phys. Le révérend Lett. 114, 160501 (2015).
https: / / doi.org/ 10.1103 / PhysRevLett.114.160501

Lieven Vandenberghe et Stephen Boyd. « Programmation semi-définie ». Revue SIAM 38, 49-95 (1996).
https: / / doi.org/ 10.1137 / 1038003

Géza Toth. « Intrication multipartite et métrologie de haute précision ». Phys. Rév. A 85, 022322 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.022322

Philipp Hyllus, Wiesław Laskowski, Roland Krischek, Christian Schwemmer, Witlef Wieczorek, Harald Weinfurter, Luca Pezzé et Augusto Smerzi. "Information Fisher et intrication multiparticules". Phys. Rév. A 85, 022321 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.022321

Géza Tóth, Tamás Vértesi, Paweł Horodecki et Ryszard Horodecki. "Activer l'utilité métrologique cachée". Phys. Le révérend Lett. 125, 020402 (2020).
https: / / doi.org/ 10.1103 / PhysRevLett.125.020402

AC Doherty, Pablo A. Parrilo et Federico M. Spedalieri. « Distinguer les États séparables et intriqués ». Phys. Le révérend Lett. 88, 187904 (2002).
https: / / doi.org/ 10.1103 / PhysRevLett.88.187904

Andrew C. Doherty, Pablo A. Parrilo et Federico M. Spedalieri. « Famille complète de critères de séparabilité ». Phys. Rév.A 69, 022308 (2004).
https: / / doi.org/ 10.1103 / PhysRevA.69.022308

Andrew C. Doherty, Pablo A. Parrilo et Federico M. Spedalieri. "Détection de l'intrication multipartite". Phys. Rév.A 71, 032333 (2005).
https: / / doi.org/ 10.1103 / PhysRevA.71.032333

Harold Ollivier et Wojciech H.Zurek. "Discorde quantique: une mesure de la quantification des corrélations". Phys. Rév. Lett. 88, 017901 (2001).
https: / / doi.org/ 10.1103 / PhysRevLett.88.017901

L. Henderson et V. Vedral. « Corrélations classiques, quantiques et totales ». J. Phys. R : Mathématiques. Gen. 34, 6899 (2001).
https:/​/​doi.org/​10.1088/​0305-4470/​34/​35/​315

Anindita Bera, Tamoghna Das, Debasis Sadhukhan, Sudipto Singha Roy, Aditi Sen(De) et Ujjwal Sen. « La discorde quantique et ses alliés : un examen des progrès récents ». Rép. Prog. Phys. 81, 024001 (2017).
https: / / doi.org/ 10.1088 / 1361-6633 / aa872f

Dénes Petz. « Covariance et informations de Fisher en mécanique quantique ». J. Phys. R : Mathématiques. Gen.35, 929 (2002).
https:/​/​doi.org/​10.1088/​0305-4470/​35/​4/​305

Paolo Gibilisco, Fumio Hiai et Dénes Petz. "Covariance quantique, informations quantiques de Fisher et relations d'incertitude". IEEETrans. Inf. Théorie 55, 439-443 (2009).
https: / / doi.org/ 10.1109 / TIT.2008.2008142

D. Petz et C. Ghinea. "Introduction à l'information quantique de Fisher". Tome 27, pages 261-281. Monde scientifique. (2011).
https: / / doi.org/ 10.1142 / 9789814338745_0015

Frank Hansen. « Informations sur l'inclinaison ajustée métrique ». Proc. Natl. Acad. Sci. États-Unis 105, 9909-9916 (2008).
https: / / doi.org/ 10.1073 / pnas.0803323105

Paolo Gibilisco, Davide Girolami et Frank Hansen. "Une approche unifiée de l'incertitude quantique locale et de la puissance interférométrique par des informations de biais ajustées métriques". Entropie 23, 263 (2021).
https: / / doi.org/ 10.3390 / e23030263

MATLAB. «9.9.0.1524771(r2020b)». The MathWorks Inc. Natick, Massachusetts (2020).

MOSEK ApS. « La boîte à outils d'optimisation MOSEK pour le manuel MATLAB. Version 9.0 ». (2019). URL : docs.mosek.com/​9.0/​toolbox/​index.html.
https://​/​docs.mosek.com/​9.0/​toolbox/​index.html

J. Löfberg. « YALMIP : Une boîte à outils pour la modélisation et l'optimisation dans MATLAB ». Dans les actes de la conférence CACSD. Taipei, Taïwan (2004).

Géza Toth. « QUBIT4MATLAB V3.0 : Un package de programmes pour la science de l'information quantique et l'optique quantique pour MATLAB ». Calculer. Phys. Commun. 179, 430-437 (2008).
https: / / doi.org/ 10.1016 / j.cpc.2008.03.007

Le package QUBIT4MATLAB est disponible sur https:/​/​www.mathworks.com/​matlabcentral/​ fileexchange/​8433, et sur la page d'accueil personnelle https:/​/​gtoth.eu/​qubit4matlab.html.
https://​/​www.mathworks.com/​matlabcentral/​fileexchange/​8433

Cité par

[1] Laurent Laflèche, « Transport quantique optimal et topologies faibles », arXiv: 2306.12944, (2023).

Les citations ci-dessus proviennent de SAO / NASA ADS (dernière mise à jour réussie 2023-10-16 14:47:44). La liste peut être incomplète car tous les éditeurs ne fournissent pas de données de citation appropriées et complètes.

Impossible de récupérer Données de référence croisée lors de la dernière tentative 2023-10-16 14:47:42: Impossible de récupérer les données citées par 10.22331 / q-2023-10-16-1143 de Crossref. C'est normal si le DOI a été enregistré récemment.

Cet article est publié dans Quantum sous le Creative Commons Attribution 4.0 International (CC BY 4.0) Licence. Le droit d'auteur reste la propriété des détenteurs d'origine tels que les auteurs ou leurs institutions.

Horodatage:

Plus de Journal quantique