Majorisation continue dans l'espace des phases quantiques

Majorisation continue dans l'espace des phases quantiques

Horodatage: 24 mai 2023, 7 h 39
Nœud source: 2674950

Zacharie Van Herstraeten1,2, Michael G.Jabbour1,3,4, et Nicolas J. Cerf1

1Centre d'information et de communication quantiques, École polytechnique de Bruxelles, CP 165/59, Université libre de Bruxelles, 1050 Bruxelles, Belgique
2Wyant College of Optical Sciences, Université de l'Arizona, 1630 E. University Blvd., Tucson, AZ 85721, États-Unis
3DAMTP, Centre des Sciences Mathématiques, Université de Cambridge, Cambridge CB3 0WA, Royaume-Uni
4Département de physique, Université technique du Danemark, 2800 Kongens Lyngby, Danemark

Vous trouvez cet article intéressant ou souhaitez en discuter? Scite ou laisse un commentaire sur SciRate.

Abstract

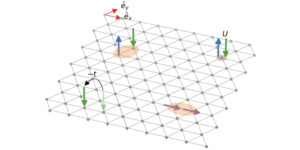
Nous explorons le rôle de la théorie de la majorisation dans l'espace des phases quantiques. À cette fin, nous nous limitons aux états quantiques avec des fonctions de Wigner positives et montrons que la version continue de la théorie de la majorisation fournit une approche élégante et très naturelle pour explorer les propriétés de la théorie de l'information des fonctions de Wigner dans l'espace des phases. Après avoir identifié tous les états purs gaussiens comme équivalents au sens précis de majorisation continue, qui peut être comprise à la lumière du théorème de Hudson, nous conjecturons une relation de majorisation fondamentale : toute fonction de Wigner positive est majorée par la fonction de Wigner d'un état pur gaussien (en particulier , l'état de vide bosonique ou l'état fondamental de l'oscillateur harmonique). En conséquence, toute fonction Schur-concave de la fonction Wigner est limitée par la valeur qu'elle prend pour l'état de vide. Cela implique à son tour que l'entropie de Wigner est limitée par sa valeur pour l'état de vide, alors que l'inverse n'est notamment pas vrai. Notre principal résultat est alors de prouver cette relation de majorisation fondamentale pour un sous-ensemble pertinent d'états quantiques positifs de Wigner qui sont des mélanges des trois états propres les plus bas de l'oscillateur harmonique. Au-delà de cela, la conjecture est également étayée par des preuves numériques. Nous concluons en discutant de certaines implications de cette conjecture dans le contexte des relations d'incertitude entropiques dans l'espace des phases.

Résumé populaire

Le principe d’incertitude est l’un des phénomènes les plus fascinants de la physique quantique. Bien qu’il puisse sembler naturel que des paires de quantités mesurables, telles que la position et l’impulsion d’une particule, puissent être prédites simultanément avec précision, la physique quantique l’interdit en réalité pour les observables non mobiles. Heisenberg et Kennard ont précisé cela en utilisant la variance de toute quantité mesurable afin de capturer son incertitude. Des années plus tard, le principe d'incertitude de Heisenberg a été reformulé en se tournant vers l'entropie comme moyen approprié de quantifier l'incertitude. Ici, nous introduisons un paradigme théorique de l'information encore plus fort pour comprendre l'incertitude des variables quantiques dans l'espace des phases, à savoir la théorie de la majorisation.

Cette théorie mathématique a été développée il y a plus d’un siècle et a été utilisée dans de nombreux domaines scientifiques, allant des statistiques à la physique. Il est remarquable qu’elle n’ait été appliquée à la physique quantique que relativement récemment, où elle s’est révélée être une approche puissante pour explorer l’intrication quantique. En tant que tel, il n’a jamais été exploité pour caractériser les densités continues qui décrivent les variables quantiques dans l’espace des phases, c’est-à-dire les fonctions de Wigner. Nous montrons que la majorisation continue est un outil approprié pour cela. L'idée principale de notre article concerne l'affirmation selon laquelle la fonction de Wigner de l'état de vide d'un mode bosonique (c'est-à-dire l'état fondamental de l'oscillateur harmonique) majore en continu toute autre fonction de Wigner, la rendant la moins incertaine dans le sens de la majorisation. .

Bien que nous exposions et discutions nos résultats dans le contexte de l’optique quantique, ils s’appliquent à n’importe quelle paire canonique et devraient donc avoir des implications dans divers domaines de la physique.

► Données BibTeX

► Références

GH Hardy, JE Littlewood et G. Pólya, « Inégalités ». La Presse de l'Universite de Cambridge, 1934.
https: / / doi.org/ 10.2307 / 3605504

AW Marshall, I. Olkin et BC Arnold, « Inégalités : théorie de la majorisation et ses applications », vol. 143. Springer, deuxième éd., 2011.
https:/​/​doi.org/​10.1007/​978-0-387-68276-1

T. Ando, ​​``Majorisation, matrices doublement stochastiques et comparaison des valeurs propres,'' Linear Algebra Appl. 118, 163-248 (1989).
https:/​/​doi.org/​10.1016/​0024-3795(89)90580-6

K. Mosler, « Majorisation dans les mesures de disparité économique », Algèbre linéaire et ses applications 199, 91-114 (1994).
https:/​/​doi.org/​10.1016/​0024-3795(94)90343-3

T. van Erven et P. Harremoës, « Divergence et majorisation de Rényi », dans le Symposium international de l'IEEE 2010 sur la théorie de l'information, pp. 1335-1339, IEEE. 2010.
https: / / doi.org/ 10.1109 / ISIT.2010.5513784

MA Alhejji et G. Smith, « A Tight Uniform Continuity Bound for Equivocation », dans le Symposium international de l'IEEE 2020 sur la théorie de l'information (ISIT), pp. 2270.
https: / / doi.org/ 10.1109 / ISIT44484.2020.9174350

MG Jabbour et N. Datta, « Une limite de continuité uniforme et étroite pour l'entropie conditionnelle Arimoto-Rényi et son extension aux états quantiques classiques », Transactions IEEE sur la théorie de l'information 68, 2169-2181 (2022).
https: / / doi.org/ 10.1109 / TIT.2022.3142812

A. Horn, « Matrices doublement stochastiques et diagonale d'une matrice de rotation », American Journal of Mathematics 76, 620-630 (1954).
https: / / doi.org/ 10.2307 / 2372705

MA Nielsen, « Conditions pour une classe de transformations par enchevêtrement », Physical Review Letters 83, 436 (1999).
https: / / doi.org/ 10.1103 / PhysRevLett.83.436

MA Nielsen et G. Vidal, « Majorisation et interconversion des états bipartites », Quantum Information and Computation 1, 76-93 (2001).
https: / / doi.org/ 10.26421 / QIC1.1-5

MA Nielsen et J. Kempe, « Les États séparables sont plus désorganisés à l'échelle mondiale que locale », Physical Review Letters 86, 5184-5187 (2001).
https: / / doi.org/ 10.1103 / PhysRevLett.86.5184

T. Hiroshima, « Critère de majorisation pour la distillabilité d'un état quantique bipartite », Physical Review Letters 91, 057902 (2003).
https: / / doi.org/ 10.1103 / PhysRevLett.91.057902

Z. Puchala, Ł. Rudnicki et K. Życzkowski, « Relations d'incertitude entropique de majorisation », Journal of Physics A : Mathematical and Theoretical 46, 272002 (2013).
https:/​/​doi.org/​10.1088/​1751-8113/​46/​27/​272002

L. Rudnicki, Z. Puchała et K. Życzkowski, « Relations d'incertitude entropique à forte majorisation », Physical Review A 89, 052115 (2014).
https: / / doi.org/ 10.1103 / PhysRevA.89.052115

L. Rudnicki, « Approche de majorisation des relations d'incertitude entropiques pour les observables à gros grains », Physical Review A 91, 032123 (2015).
https: / / doi.org/ 10.1103 / PhysRevA.91.032123

F. Brandão, M. Horodecki, N. Ng, J. Oppenheim et S. Wehner, « Les deuxièmes lois de la thermodynamique quantique », Actes de l'Académie nationale des sciences 112, 3275-3279 (2015).
https: / / doi.org/ 10.1073 / pnas.1411728112

R. García-Patrón, C. Navarrete-Benlloch, S. Lloyd, JH Shapiro et NJ Cerf, « Approche théorique de la majorisation de la conjecture d'entropie minimale du canal gaussien », Physical Review Letters 108, 110505 (2012).
https: / / doi.org/ 10.1103 / PhysRevLett.108.110505

CN Gagatsos, O. Oreshkov et NJ Cerf, « Relations de majorisation et génération d'intrication dans un séparateur de faisceau », Physical Review A 87, 042307 (2013).
https: / / doi.org/ 10.1103 / PhysRevA.87.042307

G. De Palma, D. Trevisan et V. Giovannetti, « Les états passifs optimisent la sortie des canaux quantiques gaussiens bosoniques », Transactions IEEE sur la théorie de l'information 62, 2895-2906 (2016).
https: / / doi.org/ 10.1109 / TIT.2016.2547426

MG Jabbour, R. García-Patrón et NJ Cerf, « Préservation de la majorisation des canaux bosoniques gaussiens », New Journal of Physics 18, 073047 (2016).
https:/​/​doi.org/​10.1088/​1367-2630/​18/​7/​073047

MG Jabbour et NJ Cerf, « Majorisation Fock dans les canaux quantiques bosoniques avec un environnement passif », Journal of Physics A : Mathematical and Theoretical 52, 105302 (2019).
https:/​/​doi.org/​10.1088/​1751-8121/​aaf0d2

U. Leonhardt, « L'optique quantique essentielle : des mesures quantiques aux trous noirs ». La Presse de l'Universite de Cambridge, 2010.
https: / / doi.org/ 10.1017 / CBO9780511806117

A. Hertz, MG Jabbour et NJ Cerf, « Relations d'incertitude entropie-puissance : vers une inégalité étroite pour tous les états purs gaussiens », Journal of Physics A : Mathematical and Theoretical 50, 385301 (2017).
https: / / doi.org/ 10.1088 / 1751-8121 / aa852f

A. Hertz et NJ Cerf, « Relations d'incertitude entropique à variable continue », Journal of Physics A : Mathematical and Theoretical 52, 173001 (2019).
https:/​/​doi.org/​10.1088/​1751-8121/​ab03f3

C. Weedbrook, S. Pirandola, R. García-Patrón, NJ Cerf, TC Ralph, JH Shapiro et S. Lloyd, « Informations quantiques gaussiennes », Review of Modern Physics 84, 621-669 (2012).
https: / / doi.org/ 10.1103 / RevModPhys.84.621

Z. Van Herstraeten et NJ Cerf, « Entropie quantique de Wigner », Physical Review A 104, 042211 (2021).
https: / / doi.org/ 10.1103 / PhysRevA.104.042211

FJ Narcowich, « Distributions de type $hbar$-positif et applications », Journal of mathématique physical 30, 2565-2573 (1989).
https: / / doi.org/ 10.1063 / 1.528537

T. Bröcker et R. Werner, « États mixtes avec fonctions de Wigner positives », Journal of mathématique physical 36, 62–75 (1995).
https: / / doi.org/ 10.1063 / 1.531326

RL Hudson, « Quand la densité de quasi-probabilité de Wigner est-elle non négative ? », Reports on Mathematical Physics 6, 249-252 (1974).
https:/​/​doi.org/​10.1016/​0034-4877(74)90007-X

F. Soto et P. Claverie, « Quand la fonction de Wigner des systèmes multidimensionnels est-elle non négative ? », Journal of Mathematical Physics 24, 97-100 (1983).
https: / / doi.org/ 10.1063 / 1.525607

FJ Narcowich et R. O'Connell, « Conditions nécessaires et suffisantes pour qu'une fonction d'espace de phase soit une distribution de Wigner », Physical Review A 34, 1 (1986).
https: / / doi.org/ 10.1103 / PhysRevA.34.1

A. Mandilara, E. Karpov et NJ Cerf, « Extension du théorème d'Hudson aux états quantiques mixtes », Physical Review A 79, 062302 (2009).
https: / / doi.org/ 10.1103 / PhysRevA.79.062302

A. Mandilara, E. Karpov et N. Cerf, « Limites de gaussianité pour les états quantiques mixtes avec une fonction de Wigner positive », dans Journal of Physics : Conference Series, vol. 254, p. 012011, Éditions IOP. 2010.
https:/​/​doi.org/​10.1088/​1742-6596/​254/​1/​012011

L. Wang et M. Madiman, « Au-delà de l'inégalité de puissance entropique, via des réarrangements », IEEE Transactions on Information Theory 60, 5116-5137 (2014).
https: / / doi.org/ 10.1109 / TIT.2014.2338852

GH Hardy, JE Littlewood et G. Pólya, « Quelques inégalités simples satisfaites par des fonctions convexes », Messenger of Mathematics 58, 145-152 (1929).

H. Joe, « Un ordre de dépendance pour la distribution de k-tuples, avec des applications aux jeux de loto », Revue canadienne de statistique 15, 227-238 (1987).
https: / / doi.org/ 10.2307 / 3314913

I. Schur, « Uber eine Klasse von Mittelbildungen mit Anwendungen die Determinanten », Sitzungsberichte der Berliner Mathematischen Gesellschaft 22, 416-427 (1923).

AW Roberts et DE Varberg, « Fonctions convexes ». Presse académique New York, 1973.
https:/​/​doi.org/​10.1016/​B978-0-444-89597-4.50013-5

A. Rényi, « Sur les mesures d'entropie et d'information », dans Actes du quatrième symposium de Berkeley sur les statistiques mathématiques et les probabilités, Volume 1 : Contributions à la théorie des statistiques, vol. 4, pp. 547-562, Presses de l'Université de Californie. 1961.

Y. He, AB Hamza et H. Krim, « Une mesure de divergence généralisée pour un enregistrement d'image robuste », IEEE Transactions on Signal Processing 51, 1211-1220 (2003).
https://​/​doi.org/​10.1109/​TSP.2003.810305

JV Ryff, « Orbites de fonctions $L^1$ sous transformations doublement stochastiques », Transactions de l'American Mathematical Society 117, 92-100 (1965).
https: / / doi.org/ 10.2307 / 1994198

F. Bahrami, SM Manjegani et S. Moein, « Opérateurs semi-doublement stochastiques et majorisation des fonctions intégrables », Bulletin de la Société malaisienne des sciences mathématiques 44, 693-703 (2021).
https:/​/​doi.org/​10.1007/​s40840-020-00971-2

SM Manjegani et S. Moein, « Majorisation et opérateurs semi-doublement stochastiques sur $ L^{1}(X)$ », Journal of Inequalities and Applications 2023, 1-20 (2023).
https: / / doi.org/ 10.1186 / s13660-023-02935-z

I. Białynicki-Birula et J. Mycielski, « Relations d'incertitude pour l'entropie de l'information dans la mécanique des ondes », Communications in Mathematical Physics 44, 129-132 (1975).
https: / / doi.org/ 10.1007 / BF01608825

A. Wehrl, « Propriétés générales de l'entropie », Reviews of Modern Physics 50, 221 (1978).
https: / / doi.org/ 10.1103 / RevModPhys.50.221

EH Lieb, « Preuve d'une conjecture d'entropie de Wehrl », dans Inequalities, pp. 359-365. Springer, 2002.
https:/​/​doi.org/​10.1007/​978-3-642-55925-9_30

EH Lieb et JP Solovej, « Preuve d'une conjecture d'entropie pour les états de spin cohérents de Bloch et ses généralisations », Acta Mathematica 212, 379 (2014).
https:/​/​doi.org/​10.1007/​s11511-014-0113-6

JR Johansson, PD Nation et F. Nori, « QuTiP : Un framework Python open source pour la dynamique des systèmes quantiques ouverts », Computer Physics Communications 183, 1760-1772 (2012).
https: / / doi.org/ 10.1016 / j.cpc.2012.02.021

K. Życzkowski, P. Horodecki, A. Sanpera et M. Lewenstein, « Volume de l'ensemble des états séparables », Physical Review A 58, 883 (1998).
https: / / doi.org/ 10.1103 / PhysRevA.58.883

Cité par

[1] Nuno Costa Dias et João Nuno Prata, "Sur une conjecture récente de Z. Van Herstraeten et NJ Cerf pour l'entropie quantique de Wigner", arXiv: 2303.10531, (2023).

[2] Zacharie Van Herstraeten et Nicolas J. Cerf, "Entropie quantique de Wigner", Examen physique A 104 4, 042211 (2021).

[3] Martin Gärttner, Tobias Haas et Johannes Noll, "Détection de l'intrication variable continue dans l'espace des phases avec la distribution $Q$", arXiv: 2211.17165, (2022).

Les citations ci-dessus proviennent de SAO / NASA ADS (dernière mise à jour réussie 2023-05-24 23:55:18). La liste peut être incomplète car tous les éditeurs ne fournissent pas de données de citation appropriées et complètes.

On Service cité par Crossref aucune donnée sur la citation des œuvres n'a été trouvée (dernière tentative 2023-05-24 23:55:17).

Cet article est publié dans Quantum sous le Creative Commons Attribution 4.0 International (CC BY 4.0) Licence. Le droit d'auteur reste la propriété des détenteurs d'origine tels que les auteurs ou leurs institutions.

Horodatage:

Plus de Journal quantique