1مرکز اطلاعات و ارتباطات کوانتومی، École polytechnique de Bruxelles, CP 165/59, Université libre de Bruxelles, 1050 Brussels, Belgium
2کالج علوم نوری وایانت، دانشگاه آریزونا، 1630 E. University Blvd., Tucson, AZ 85721, USA
3DAMTP، مرکز علوم ریاضی، دانشگاه کمبریج، کمبریج CB3 0WA، بریتانیا
4گروه فیزیک، دانشگاه فنی دانمارک، 2800 Kongens Lyngby، دانمارک
این مقاله را جالب می دانید یا می خواهید بحث کنید؟ SciRate را ذکر کنید یا در SciRate نظر بدهید.
چکیده
ما نقش نظریه عمدهسازی را در فضای فاز کوانتومی بررسی میکنیم. برای این منظور، ما خود را به حالتهای کوانتومی با توابع ویگنر مثبت محدود میکنیم و نشان میدهیم که نسخه پیوسته نظریه عمدهسازی رویکردی ظریف و بسیار طبیعی برای کاوش ویژگیهای نظری اطلاعات توابع ویگنر در فضای فاز ارائه میکند. پس از شناسایی همه حالات خالص گاوسی به عنوان معادل در معنای دقیق عمدهسازی پیوسته، که میتوان آن را در پرتو قضیه هادسون فهمید، یک رابطه عمدهسازی اساسی را حدس میزنیم: هر تابع ویگنر مثبت با تابع ویگنر یک حالت خالص گاوسی بزرگ میشود (به ویژه ، حالت خلاء بوزونی یا حالت پایه نوسانگر هارمونیک). در نتیجه، هر تابع Schur-concave تابع ویگنر با مقداری که برای حالت خلاء می گیرد محدودتر است. این به نوبه خود نشان می دهد که آنتروپی ویگنر با مقدار آن برای حالت خلاء محدودتر است، در حالی که عکس این موضوع به طور قابل توجهی درست نیست. نتیجه اصلی ما این است که این رابطه عمدهسازی اساسی را برای زیرمجموعهای از حالتهای کوانتومی مثبت ویگنر که مخلوطی از سه پایینترین حالت ویژه نوسانگر هارمونیک هستند، اثبات کنیم. فراتر از آن، این حدس با شواهد عددی نیز پشتیبانی می شود. ما با بحث در مورد برخی پیامدهای این حدس در زمینه روابط عدم قطعیت آنتروپیک در فضای فاز نتیجه گیری می کنیم.
خلاصه محبوب
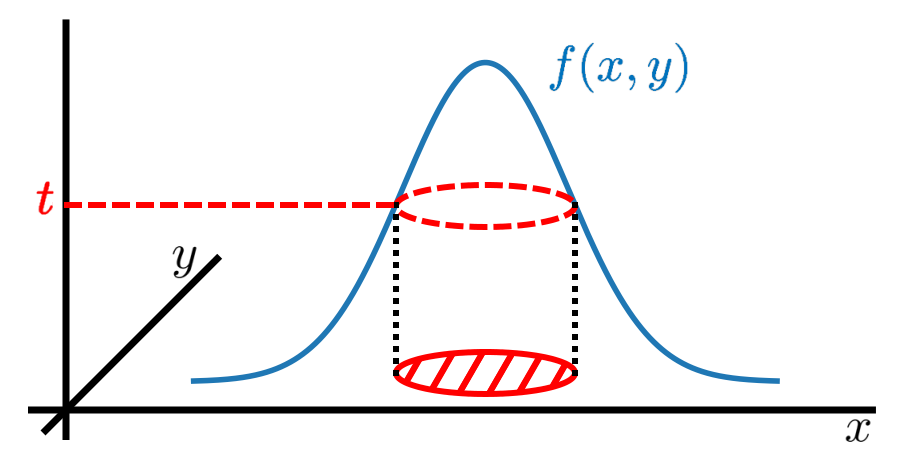
این نظریه ریاضی بیش از یک قرن پیش توسعه یافته است و در زمینه های علمی متعددی از آمار گرفته تا فیزیک مورد استفاده قرار گرفته است. قابل توجه است که این روش به تازگی در فیزیک کوانتومی به کار گرفته شده است، جایی که نشان داده شده است که یک رویکرد قدرتمند برای کاوش درهم تنیدگی کوانتومی است. به این ترتیب، هرگز برای توصیف چگالی های پیوسته که متغیرهای کوانتومی را در فضای فاز توصیف می کنند، یعنی توابع ویگنر، استفاده نشده است. ما نشان میدهیم که عمدهسازی پیوسته ابزار مناسبی برای این کار است. محور اصلی مقاله ما به این بیانیه مربوط می شود که تابع ویگنر از حالت خلاء حالت بوزونی (یعنی حالت پایه نوسانگر هارمونیک) هر تابع ویگنر دیگر را به صورت پیوسته بزرگ می کند، و باعث می شود که آن را از نظر بزرگ شدن نامطمئن تر کند. .
در حالی که ما نتایج خود را در زمینه اپتیک کوانتومی نشان میدهیم و مورد بحث قرار میدهیم، آنها به هر جفت متعارفی منتقل میشوند و بنابراین باید پیامدهایی در حوزههای مختلف فیزیک داشته باشند.
► داده های BibTeX
◄ مراجع
[1] GH Hardy، JE Littlewood، و G. Pólya، "نابرابری ها". انتشارات دانشگاه کمبریج، 1934.
https://doi.org/10.2307/3605504
[2] AW Marshall, I. Olkin, and BC Arnold, ``Inequalities: Theory of Majorization and its Applications, vol. 143. اسپرینگر، ویرایش دوم، 2011.
https://doi.org/10.1007/978-0-387-68276-1
[3] T. Ando، "Majorization، ماتریس های تصادفی مضاعف، و مقایسه مقادیر ویژه"، Linear Algebra Appl. 118، 163-248 (1989).
https://doi.org/10.1016/0024-3795(89)90580-6
[4] K. Mosler، "عمدیت در معیارهای نابرابری اقتصادی"، جبر خطی و کاربردهای آن 199، 91-114 (1994).
https://doi.org/10.1016/0024-3795(94)90343-3
[5] T. van Erven and P. Harremoes, "Rényi divergence and majorization" در 2010 IEEE International Symposium on Information Theory, pp. 1335-1339, IEEE. 2010.
https://doi.org/10.1109/ISIT.2010.5513784
[6] MA Alhejji و G. Smith، "A Tight Uniform Continuity Bound for Equivocation" در سال 2020 سمپوزیوم بین المللی IEEE در نظریه اطلاعات (ISIT)، صفحات 2270-2274. 2020.
https://doi.org/10.1109/ISIT44484.2020.9174350
[7] MG Jabbour و N. Datta، "یک محدودیت یکنواخت محکم برای آنتروپی شرطی Arimoto-Rényi و گسترش آن به حالت های کوانتومی کلاسیک،" IEEE Transactions on Information Theory 68, 2169-2181 (2022).
https://doi.org/10.1109/TIT.2022.3142812
[8] A. Horn، "ماتریس های تصادفی مضاعف و مورب یک ماتریس چرخش"، مجله آمریکایی ریاضیات 76، 620-630 (1954).
https://doi.org/10.2307/2372705
[9] MA Nielsen، "شرایط برای طبقه ای از تبدیلات درهم تنیدگی"، نامه های مروری فیزیکی 83، 436 (1999).
https://doi.org/10.1103/PhysRevLett.83.436
[10] MA Nielsen و G. Vidal، "عمده سازی و تبدیل حالت های دوبخشی"، اطلاعات کوانتومی و محاسبات 1، 76-93 (2001).
https://doi.org/10.26421/QIC1.1-5
[11] MA Nielsen و J. Kempe، "کشورهای جداشدنی در سطح جهانی بیش از محلی نابسامان هستند"، Physical Review Letters 86، 5184-5187 (2001).
https://doi.org/10.1103/PhysRevLett.86.5184
[12] تی. هیروشیما، "معیار اصلی برای تقطیر پذیری یک حالت کوانتومی دوبخشی"، نامه های بررسی فیزیکی 91، 057902 (2003).
https://doi.org/10.1103/PhysRevLett.91.057902
[13] Z. Puchała، Ł. رودنیکی، و کی.
https://doi.org/10.1088/1751-8113/46/27/272002
[14] ال. رودنیکی، ز. پوچالا، و کی.
https://doi.org/10.1103/PhysRevA.89.052115
[15] ال. رودنیکی، «رویکرد عمدهسازی به روابط عدم قطعیت آنتروپیک برای مشاهدهپذیرهای درشت دانه»، بررسی فیزیکی A 91، 032123 (2015).
https://doi.org/10.1103/PhysRevA.91.032123
[16] F. Brandão، M. Horodecki، N. Ng، J. Oppenheim، و S. Wehner، "قوانین دوم ترمودینامیک کوانتومی،" مجموعه مقالات آکادمی ملی علوم 112، 3275-3279 (2015).
https://doi.org/10.1073/pnas.1411728112
[17] R. García-Patrón، C. Navarrete-Benlloch، S. Lloyd، JH Shapiro، و NJ Cerf، «رویکرد تئوری عمدهسازی به حدسی حداقل آنتروپی کانال گاوسی»، نامههای بازبینی فیزیکی 108، 110505 (2012).
https://doi.org/10.1103/PhysRevLett.108.110505
[18] CN Gagatsos، O. Oreshkov، و NJ Cerf، "روابط اصلی و تولید درهم تنیدگی در شکاف پرتو"، بررسی فیزیکی A 87، 042307 (2013).
https://doi.org/10.1103/PhysRevA.87.042307
[19] G. De Palma، D. Trevisan و V. Giovannetti، "حالت های غیرفعال خروجی کانال های کوانتومی گاوسی بوزونی را بهینه می کنند"، IEEE Transactions on Information Theory 62، 2895-2906 (2016).
https://doi.org/10.1109/TIT.2016.2547426
[20] MG Jabbour، R. García-Patrón، و NJ Cerf، "حفظ عمده کانال های بوزونی گاوسی"، مجله جدید فیزیک 18، 073047 (2016).
https://doi.org/10.1088/1367-2630/18/7/073047
[21] MG Jabbour و NJ Cerf، "عمده سازی فوک در کانال های کوانتومی بوزونی با یک محیط غیرفعال"، مجله فیزیک A: ریاضی و نظری 52، 105302 (2019).
https://doi.org/10.1088/1751-8121/aaf0d2
[22] U. Leonhardt، "اپتیک کوانتومی ضروری: از اندازه گیری های کوانتومی تا سیاهچاله ها". انتشارات دانشگاه کمبریج، 2010.
https://doi.org/10.1017/CBO9780511806117
[23] A. Hertz، MG Jabbour و NJ Cerf، "روابط عدم قطعیت آنتروپی-قدرت: به سمت یک نابرابری فشرده برای همه حالات خالص گاوسی"، مجله فیزیک A: ریاضی و نظری 50، 385301 (2017).
https://doi.org/10.1088/1751-8121/aa852f
[24] A. Hertz و NJ Cerf، "روابط عدم قطعیت آنتروپیک متغیر پیوسته"، مجله فیزیک A: ریاضی و نظری 52، 173001 (2019).
https://doi.org/10.1088/1751-8121/ab03f3
[25] C. Weedbrook، S. Pirandola، R. García-Patrón، NJ Cerf، TC Ralph، JH Shapiro، و S. Lloyd، "اطلاعات کوانتومی گاوسی،" بررسی فیزیک مدرن 84، 621-669 (2012).
https://doi.org/10.1103/RevModPhys.84.621
[26] Z. Van Herstraeten و NJ Cerf، «آنتروپی کوانتومی ویگنر»، Physical Review A 104, 042211 (2021).
https://doi.org/10.1103/PhysRevA.104.042211
[27] FJ Narcowich، "توزیعات $hbar$-نوع و برنامه های کاربردی"، مجله فیزیک ریاضی 30، 2565-2573 (1989).
https://doi.org/10.1063/1.528537
[28] T. Bröcker و R. Werner، "حالت های مخلوط با توابع مثبت ویگنر"، مجله فیزیک ریاضی 36، 62-75 (1995).
https://doi.org/10.1063/1.531326
[29] RL هادسون، «چه زمانی چگالی شبه احتمال ویگنر غیر منفی است؟»، گزارشهای مربوط به فیزیک ریاضی 6، 249-252 (1974).
https://doi.org/10.1016/0034-4877(74)90007-X
[30] F. Soto و P. Claverie، "چه زمانی تابع ویگنر سیستم های چند بعدی غیر منفی است؟"، مجله فیزیک ریاضی 24، 97-100 (1983).
https://doi.org/10.1063/1.525607
[31] FJ Narcowich و R. O'Connell، "شرایط لازم و کافی برای یک تابع فضای فاز به عنوان توزیع ویگنر"، Physical Review A 34, 1 (1986).
https://doi.org/10.1103/PhysRevA.34.1
[32] A. Mandilara، E. Karpov، و NJ Cerf، "بسط قضیه هادسون به حالت های کوانتومی مختلط"، Physical Review A 79, 062302 (2009).
https://doi.org/10.1103/PhysRevA.79.062302
[33] A. Mandilara، E. Karpov و N. Cerf، "مرزهای گاوسی برای حالات مخلوط کوانتومی با تابع ویگنر مثبت،" در Journal of Physics: Conference Series, vol. 254، ص. 012011، انتشارات IOP. 2010.
https://doi.org/10.1088/1742-6596/254/1/012011
[34] L. Wang و M. Madiman، "فراتر از نابرابری قدرت آنتروپی، از طریق بازآرایی"، IEEE Transactions on Information Theory 60, 5116-5137 (2014).
https://doi.org/10.1109/TIT.2014.2338852
[35] GH Hardy، JE Littlewood، و G. Pólya، "برخی نابرابری های ساده برآورده شده توسط توابع محدب"، رسول ریاضیات 58، 145-152 (1929).
[36] H. Joe، "ترتیب وابستگی برای توزیع k-tuples، با کاربرد در بازی های لوتو"، مجله Canadian Statistics 15, 227-238 (1987).
https://doi.org/10.2307/3314913
[37] I. Schur، «Uber eine Klasse von Mittelbildungen mit Anwendungen die Determinanten»، Sitzungsberichte der Berliner Mathematischen Gesellschaft 22, 416–427 (1923).
[38] AW Roberts و DE Varberg، "توابع محدب،". انتشارات آکادمیک نیویورک، 1973.
https://doi.org/10.1016/B978-0-444-89597-4.50013-5
[39] A. Rényi، «درباره معیارهای آنتروپی و اطلاعات،» در مجموعه مقالات چهارمین سمپوزیوم برکلی در مورد آمار ریاضی و احتمال، جلد 1: مشارکت در نظریه آمار، جلد. 4، صفحات 547-562، انتشارات دانشگاه کالیفرنیا. 1961.
[40] Y. He، AB Hamza و H. Krim، "معیار واگرایی تعمیم یافته برای ثبت تصویر قوی"، IEEE Transactions on Signal Processing 51، 1211-1220 (2003).
https://doi.org/10.1109/TSP.2003.810305
[41] JV Ryff، "مدارهای $L^1$-توابع تحت تبدیل های تصادفی مضاعف"، تراکنش های انجمن ریاضی آمریکا 117، 92-100 (1965).
https://doi.org/10.2307/1994198
[42] F. بهرامی، SM Manjegani و S. Moein، «عملگرهای تصادفی نیمه مضاعف و عمدهسازی توابع ادغامپذیر»، بولتن انجمن علوم ریاضی مالزی 44، 693-703 (2021).
https://doi.org/10.1007/s40840-020-00971-2
[43] SM Manjegani و S. Moein، "عمده سازی و عملگرهای نیمه تصادفی در $ L^{1}(X)$،" مجله نابرابری ها و کاربردها 2023، 1-20 (2023).
https://doi.org/10.1186/s13660-023-02935-z
[44] I. Białynicki-Birula و J. Mycielski، "روابط عدم قطعیت برای آنتروپی اطلاعات در مکانیک موج،" ارتباطات در فیزیک ریاضی 44، 129-132 (1975).
https://doi.org/10.1007/BF01608825
[45] A. Wehrl، "خواص کلی آنتروپی"، Reviews of Modern Physics 50, 221 (1978).
https://doi.org/10.1103/RevModPhys.50.221
[46] EH Lieb، "اثبات حدس آنتروپی Wehrl" در Inequalities، ص 359-365. اسپرینگر، 2002.
https://doi.org/10.1007/978-3-642-55925-9_30
[47] EH Lieb و JP Solovej، «اثبات حدس آنتروپی برای حالتهای اسپین منسجم بلوخ و تعمیمهای آن»، Acta Mathematica 212، 379 (2014).
https://doi.org/10.1007/s11511-014-0113-6
[48] JR Johansson، PD Nation، و F. Nori، "QuTiP: چارچوب پایتون منبع باز برای دینامیک سیستم های کوانتومی باز،" ارتباطات فیزیک کامپیوتر 183، 1760-1772 (2012).
https://doi.org/10.1016/j.cpc.2012.02.021
ذکر شده توسط
[1] Nuno Costa Dias و João Nuno Prata، "در یک حدس اخیر توسط Z. Van Herstraeten و NJ Cerf برای آنتروپی ویگنر کوانتومی"، arXiv: 2303.10531, (2023).
[2] Zacharie Van Herstraeten و Nicolas J. Cerf، "آنتروپی کوانتوم ویگنر"، بررسی فیزیکی A 104 4, 042211 (2021).
[3] مارتین گارتنر، توبیاس هاس و یوهانس نول، "تشخیص درهم تنیدگی متغیر پیوسته در فضای فاز با توزیع $Q$"، arXiv: 2211.17165, (2022).
نقل قول های بالا از SAO/NASA Ads (آخرین به روز رسانی با موفقیت 2023-05-24 23:55:18). فهرست ممکن است ناقص باشد زیرا همه ناشران داده های استنادی مناسب و کاملی را ارائه نمی دهند.
On سرویس استناد شده توسط Crossref هیچ داده ای در مورد استناد به آثار یافت نشد (آخرین تلاش 2023-05-24 23:55:17).
این مقاله در Quantum تحت عنوان منتشر شده است Creative Commons Attribution 4.0 International (CC BY 4.0) مجوز. حق چاپ نزد دارندگان حق چاپ اصلی مانند نویسندگان یا مؤسسات آنها باقی می ماند.
- محتوای مبتنی بر SEO و توزیع روابط عمومی. امروز تقویت شوید.
- PlatoAiStream. Web3 Data Intelligence دانش تقویت شده دسترسی به اینجا.
- ضرب کردن آینده با آدرین اشلی. دسترسی به اینجا.
- خرید و فروش سهام در شرکت های PRE-IPO با PREIPO®. دسترسی به اینجا.
- منبع: https://quantum-journal.org/papers/q-2023-05-24-1021/
- : دارد
- :است
- :نه
- :جایی که
- ][پ
- 1
- 10
- 11
- 12
- 13
- 14
- ٪۱۰۰
- 17
- 1934
- 1994
- 1998
- 1999
- 20
- 2001
- 2011
- 2012
- 2013
- 2014
- 2015
- 2016
- 2017
- 2019
- 2020
- 2021
- 2022
- 2023
- 22
- 23
- 24
- 26
- 27
- 28
- 30
- 39
- 40
- 49
- 50
- 60
- 7
- 8
- 84
- 87
- 9
- 91
- a
- بالاتر
- چکیده
- دانشگاهی
- دانشگاه
- دسترسی
- به درستی
- واقعا
- وابستگی ها
- پس از
- پیش
- معرفی
- همچنین
- امریکایی
- an
- و
- هر
- برنامه های کاربردی
- اعمال می شود
- روش
- هستند
- مناطق
- آریزونا
- AS
- نویسنده
- نویسندگان
- BE
- پرتو
- بوده
- برکلی
- خارج از
- سیاه پوست
- سیاه چاله ها
- بسته
- شکستن
- بروکسل
- پژوهشنامه
- by
- کالیفرنیا
- کمبریج
- CAN
- کانادایی
- گرفتن
- حمل
- مرکز
- قرن
- کانال
- کانال
- مشخص کردن
- کلاس
- منسجم
- کالج
- توضیح
- مردم عادی
- ارتباط
- ارتباطات
- مقایسه
- کامل
- محاسبه
- کامپیوتر
- نگرانی ها
- نتیجه گیری
- شرایط
- کنفرانس
- حدس
- زمینه
- مداوم
- مشارکت
- محدب
- حق چاپ
- میتوانست
- داده ها
- آن
- دانمارک
- چگالی
- وابستگی
- توصیف
- توسعه
- مردن
- بحث و تبادل نظر
- بحث در مورد
- توزیع
- واگرایی
- دوبار
- دینامیک
- e
- اقتصادی
- ed
- محیط
- معادل
- به خصوص
- اتر (ETH)
- مدرک
- سوء استفاده قرار گیرد
- اکتشاف
- بررسی
- گسترش
- شگفت انگیز
- زمینه
- مناسب
- برای
- یافت
- چهارم
- چارچوب
- از جانب
- تابع
- توابع
- اساسی
- بازیها
- نسل
- در سطح جهانی
- زمین
- دانشگاه هاروارد
- آیا
- he
- اینجا کلیک نمایید
- هرتز
- دارندگان
- سوراخ
- HTTPS
- i
- شناسایی
- IEEE
- تصویر
- پیامدهای
- in
- نابرابری
- نابرابری
- اطلاعات
- موسسات
- جالب
- بین المللی
- معرفی
- IT
- ITS
- جاوا اسکریپت
- روزنامه
- نام
- بعد
- قوانین
- ترک کردن
- کمتر
- مجوز
- سبک
- فهرست
- به صورت محلی
- پایین ترین
- ساخته
- اصلی
- ساخت
- مالزی
- مارتین
- ریاضی
- ریاضیات
- ماتریس
- حداکثر عرض
- ممکن است..
- به معنی
- اندازه
- اندازه گیری
- معیارهای
- مکانیک
- رسول
- مایکل
- حد اقل
- MIT
- مخلوط
- حالت
- مدرن
- حرکت
- ماه
- بیش
- اکثر
- از جمله
- ملت
- ملی
- طبیعی
- هرگز
- جدید
- نیویورک
- نیکولا
- نه
- به ویژه
- متعدد
- of
- on
- ONE
- فقط
- باز کن
- منبع باز
- اپراتور
- اپتیک
- بهینه سازی
- or
- سفارش
- اصلی
- دیگر
- ما
- خودمان
- تولید
- روی
- جفت
- جفت
- مقاله
- نمونه
- ذره
- غیر فعال
- فاز
- فیزیکی
- فیزیک
- افلاطون
- هوش داده افلاطون
- PlatoData
- موقعیت
- مثبت
- قدرت
- قوی
- دقیق
- پیش بینی
- حفظ
- فشار
- اصل
- احتمال
- اقدامات
- در حال پردازش
- مناسب
- املاک
- ثابت كردن
- ارائه
- فراهم می کند
- منتشر شده
- ناشر
- ناشران
- انتشار
- هدف
- پــایتــون
- مقدار
- کوانتومی
- درهمتنیدگی کوانتومی
- اطلاعات کوانتومی
- اپتیک کوانتومی
- فیزیک کوانتوم
- سیستم های کوانتومی
- اعم
- تنظیم مجدد
- اخیر
- تازه
- منابع
- ثبت
- ارتباط
- روابط
- نسبتا
- مربوط
- بقایای
- گزارش ها
- محدود کردن
- نتیجه
- نتایج
- این فایل نقد می نویسید:
- بررسی
- تنومند
- نقش
- s
- راضی
- علم
- علوم
- دوم
- به نظر می رسد
- حس
- سلسله
- تنظیم
- باید
- نشان
- نشان داده شده
- سیگنال
- ساده
- به طور همزمان
- جامعه
- برخی از
- فضا
- چرخش
- دولت
- بیانیه
- ایالات
- ارقام
- قوی
- موفقیت
- چنین
- کافی
- مناسب
- پشتیبانی
- بزم پس از شام
- سیستم های
- طول می کشد
- فنی
- نسبت به
- که
- La
- شان
- سپس
- نظری
- نظریه
- از این رو
- آنها
- این
- سه
- عنوان
- به
- ابزار
- طرف
- معاملات
- تحولات
- درست
- دور زدن
- عطف
- نوع
- مردد
- تردید
- زیر
- درک
- فهمید
- متحد
- دانشگاه
- دانشگاه کالیفرنیا
- دانشگاه کمبریج
- به روز شده
- URL
- استفاده
- خلاء
- ارزش
- مختلف
- نسخه
- بسیار
- از طريق
- حجم
- از
- W
- می خواهم
- بود
- موج
- we
- که
- در حین
- با
- با این نسخهها کار
- X
- سال
- سال
- هنوز
- نیویورک
- زفیرنت