Distancia cuántica de Wasserstein basada en una optimización sobre estados separables

Distancia cuántica de Wasserstein basada en una optimización sobre estados separables

Marca de tiempo: 16 de octubre de 2023 10:35 a. M.
Nodo de origen: 2938953

Géza Tóth1,2,3,4,5 y József Pitrik5,6,7

1Física Teórica, Universidad del País Vasco UPV/EHU, ES-48080 Bilbao, España
2EHU Quantum Center, Universidad del País Vasco UPV/EHU, Barrio Sarriena s/n, ES-48940 Leioa, Vizcaya, España
3Centro Internacional de Física de Donostia (DIPC), ES-20080 San Sebastián, España
4IKERBASQUE, Fundación Vasca para la Ciencia, ES-48011 Bilbao, España
5Instituto de Física y Óptica del Estado Sólido, Centro de Investigación de Física Wigner, HU-1525 Budapest, Hungría
6Instituto de Matemáticas Alfréd Rényi, Reáltanoda u. 13-15., HU-1053 Budapest, Hungría
7Departamento de Análisis e Investigación Operativa, Instituto de Matemáticas, Universidad de Tecnología y Economía de Budapest, Müegyetem rkp. 3., HU-1111 Budapest, Hungría

¿Encuentra este documento interesante o quiere discutirlo? Scite o deje un comentario en SciRate.

Resumen

Definimos la distancia cuántica de Wasserstein de manera que la optimización del acoplamiento se lleve a cabo sobre estados bipartitos separables en lugar de estados cuánticos bipartitos en general, y examinamos sus propiedades. Sorprendentemente, encontramos que la autodistancia está relacionada con la información cuántica de Fisher. Presentamos un mapa de transporte correspondiente a un estado separable bipartito óptimo. Discutimos cómo la distancia cuántica de Wasserstein introducida está relacionada con los criterios que detectan el entrelazamiento cuántico. Definimos cantidades similares a varianzas que se pueden obtener a partir de la distancia cuántica de Wasserstein reemplazando la minimización de los estados cuánticos por una maximización. Ampliamos nuestros resultados a una familia de cantidades de información cuántica generalizada de Fisher.

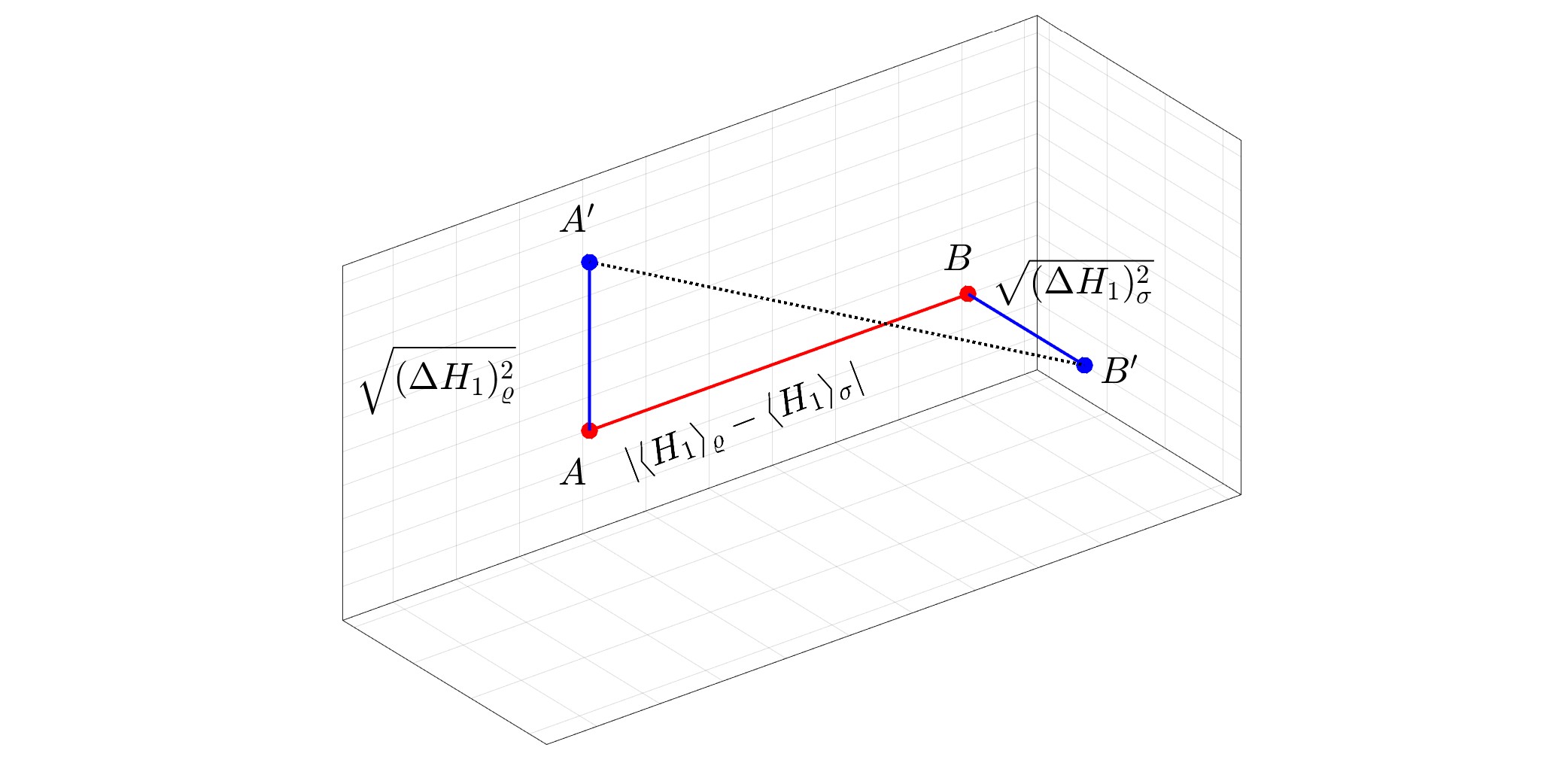
Imagen de portada: Representación geométrica de la distancia cuántica de Wasserstein entre un estado puro $varrho$ y un estado mixto $sigma$ para $N=1.$ La distancia cuántica de Wasserstein es igual a $1/sqrt2$ multiplicado por la distancia euclidiana habitual entre $A'$ y $B'.$

Resumen popular

En la vida cotidiana, la distancia entre dos ciudades nos dice cuántos kilómetros tenemos que recorrer de una a otra. También es posible caracterizar la facilidad con la que podemos desplazarnos de una ciudad a otra midiendo el consumo de combustible durante nuestro trayecto. Este último es más informativo en el sentido de que refleja el costo del viaje relacionado con la topografía de la carretera, es decir, es sensible a la métrica subyacente. A continuación, imaginemos que necesitamos mover un montón de arena de un lugar a otro y que el nuevo montón podría tener una forma diferente. En este caso, nuevamente, podemos caracterizar el esfuerzo de mover la arena por el costo del transporte.

Las distancias juegan un papel central en matemáticas, física e ingeniería. Un problema fundamental en probabilidad y estadística es encontrar medidas útiles de distancia entre dos distribuciones de probabilidad. Desafortunadamente, muchas nociones de distancia entre distribuciones de probabilidad, digamos p(x) y q(x), son máximas si no se superponen entre sí, es decir, una siempre es cero cuando la otra es distinta de cero. Esto no es práctico para muchas aplicaciones. Por ejemplo, volviendo a la analogía de la arena, dos montones de arena que no se superponen parecen estar igualmente lejos uno del otro, independientemente de si su distancia es de 10 o 100 km. La teoría del transporte óptimo es una forma de construir una noción alternativa de distancia entre distribuciones de probabilidad, la llamada distancia de Wasserstein. Puede ser no máximo incluso si las distribuciones no se superponen entre sí, es sensible a la métrica subyacente (es decir, el costo del transporte) y, esencialmente, expresa el esfuerzo que necesitamos para mover uno al otro. como si fueran colinas de arena.

Recientemente, la distancia de Wasserstein cuántica se ha definido generalizando la distancia de Wasserstein clásica. Se basa en la minimización de una función de costes sobre los estados cuánticos de un sistema cuántico bipartito. Tiene la propiedad análoga a la mencionada anteriormente en el mundo cuántico. Puede ser no máximo para estados ortogonales, lo que resulta útil, por ejemplo, cuando necesitamos enseñar datos cuánticos a un algoritmo.

Como podemos esperar, la distancia cuántica de Wasserstein también tiene propiedades muy diferentes a las de su contraparte clásica. Por ejemplo, cuando medimos la distancia de un estado cuántico a sí mismo, puede ser distinta de cero. Si bien esto ya resulta desconcertante, también se ha descubierto que la autodistancia está relacionada con la información sesgada de Wigner-Yanase, introducida en 1963 por el premio Nobel EP Wigner, quien tiene contribuciones vitales a los fundamentos de la física cuántica y MM Yanase.

En nuestro artículo, analizamos este misterioso hallazgo desde otra dirección. La minimización mencionada anteriormente la restringimos a los llamados estados separables. Estos son los estados cuánticos que no contienen entrelazamiento. Encontramos que la autodistancia se convierte en la información cuántica de Fisher, una cantidad central en la metrología cuántica y la teoría de la estimación cuántica, y que aparece, por ejemplo, en el famoso límite de Cramer-Rao. Al examinar las propiedades de dicha distancia de Wasserstein, nuestro trabajo allana el camino para conectar la teoría de la distancia de Wasserstein cuántica con la teoría del entrelazamiento cuántico.

► datos BibTeX

► referencias

[ 1 ] G. Monge. “Mémoire sur la théory des déblais et des remblais”. Memorias de la Academia Real de Ciencias de París (1781).

[ 2 ] L. Kantorovich. “Sobre la translocación de masas”. Ciencias de la gestión 5, 1–4 (1958). URL: http://​/​www.jstor.org/​stable/​2626967.
http: / / www.jstor.org/ stable / 2626967

[ 3 ] Emmanuel Boissard, Thibaut Le Gouic y Jean-Michel Loubes. “Plantilla de estimación de distribución con métricas de Wasserstein”. Bernoulli 21, 740–759 (2015).
https://​/​doi.org/​10.3150/​13-bej585

[ 4 ] Oleg Butkovski. “Tasas subgeométricas de convergencia de los procesos de Markov en la métrica de Wasserstein”. Ana. Aplica. Probablemente. 24, 526–552 (2014).
https://​/​doi.org/​10.1214/​13-AAP922

[ 5 ] M. Hairer, J.-C. Mattingly y M. Scheutzow. "Acoplamiento asintótico y una forma general del teorema de Harris con aplicaciones a ecuaciones de retardo estocástico". Probablemente. Relación teórica. Campos 149, 223–259 (2011).
https:/​/​doi.org/​10.1007/​s00440-009-0250-6

[ 6 ] M. Hairer y JC Mattingly. "Brechas espectrales en distancias de Wasserstein y las ecuaciones estocásticas 2D de Navier-Stokes". Ana. Probablemente. 36, 2050-2091 (2008).
https: / / doi.org/ 10.1214 / 08-AOP392

[ 7 ] A. Figalli, F. Maggi y A. Pratelli. “Un enfoque del transporte masivo para las desigualdades isoperimétricas cuantitativas”. Inventar. Matemáticas. 182, 167–211. (2010).
https: / / doi.org/ 10.1007 / s00222-010-0261-z

[ 8 ] A. Figalli y F. Maggi. “Sobre la forma de gotas líquidas y cristales en el régimen de masa pequeña”. Arco. Racionar. Mec. Anal. 201, 143–207 (2011).
https: / / doi.org/ 10.1007 / s00205-010-0383-x

[ 9 ] J. Lott y C. Villani. “Curvatura de Ricci para espacios de medidas métricas mediante transporte óptimo”. Ana. de Matemáticas. 169 (3), 903–991 (2009).
https:/​/​doi.org/​10.48550/​arXiv.math/​0412127

[ 10 ] Max-K. von Renesse y Karl-Theodor Sturm. “Desigualdades de transporte, estimaciones de gradientes, entropía y curvatura de Ricci”. Com. Pura aplicación. Matemáticas. 58, 923–940 (2005).
https: / / doi.org/ 10.1002 / cpa.20060

[ 11 ] Karl-Theodor Sturm. “Sobre la geometría de los espacios de medidas métricas I”. Acta Matemáticas. 196, 65-131 (2006).
https:/​/​doi.org/​10.1007/​s11511-006-0002-8

[ 12 ] Karl-Theodor Sturm. “Sobre la geometría de los espacios de medidas métricas II”. Acta Matemáticas. 196, 133-177 (2006).
https:/​/​doi.org/​10.1007/​s11511-006-0003-7

[ 13 ] Benoı̂t Kloeckner. “Un estudio geométrico de los espacios de Wasserstein: espacios euclidianos”. Annali della Scuola Normale Superiore di Pisa - Classe di Scienze, Scuola Normale Superiore 2010 IX (2), 297–323 (2010).
https: / / doi.org/ 10.2422 / 2036-2145.2010.2.03

[ 14 ] György Pál Gehér, Tamás Titkos y Dániel Virosztek. "Sobre incrustaciones isométricas de espacios de Wasserstein: el caso discreto". J. Matemáticas. Anal. Aplica. 480, 123435 (2019).
https://​/​doi.org/​10.1016/​j.jmaa.2019.123435

[ 15 ] György Pál Gehér, T. Titkos, Dániel Virosztek. “Estudio isométrico de los espacios de Wasserstein – la recta real”. Trans. América. Matemáticas. Soc. 373, 5855–5883 (2020).
https: / / doi.org/ 10.1090 / tran / 8113

[ 16 ] György Pál Gehér, Tamás Titkos y Dániel Virosztek. “El grupo de isometría de los espacios de Wasserstein: el caso hilbertiano”. J. Londres. Matemáticas. Soc. 106, 3865–3894 (2022).
https://​/​doi.org/​10.1112/​jlms.12676

[ 17 ] György Pál Gehér, Tamás Titkos y Dániel Virosztek. “Rigidez isométrica de toros y esferas de Wasserstein”. Matemáticas 69, 20–32 (2023).
https://​/​doi.org/​10.1112/​mtk.12174

[ 18 ] Gergely Kiss y Tamás Titkos. “Rigidez isométrica de espacios de Wasserstein: el caso gráfico métrico”. Proc. Soy. Matemáticas. Soc. 150, 4083–4097 (2022).
https: / / doi.org/ 10.1090 / proc / 15977

[ 19 ] György Pál Gehér, Tamás Titkos y Dániel Virosztek. “Sobre el exótico flujo isométrico del espacio cuadrático de Wasserstein sobre la recta real”. Aplicación de álgebra lineal. (2023).
https: / / doi.org/ 10.1016 / j.laa.2023.02.016

[ 20 ] S. Kolouri, SR Park y GK Rohde. “La transformada de distribución acumulativa de radón y su aplicación a la clasificación de imágenes”. Traducción IEEE. Proceso de imagen. 25, 920–934 (2016).
https: / / doi.org/ 10.1109 / TIP.2015.2509419

[ 21 ] W. Wang, D. Slepc̆ev, S. Basu, JA Ozolek y GK Rohde. "Un marco de transporte lineal óptimo para cuantificar y visualizar variaciones en conjuntos de imágenes". En t. J. Computación. Vis. 101, 254–269 (2013).
https: / / doi.org/ 10.1007 / s11263-012-0566-z

[ 22 ] S. Kolouri, S. Park, M. Thorpe, D. Slepc̆ev, GK Rohde. “Transporte de masa óptimo: procesamiento de señales y aplicaciones de aprendizaje automático”. Revista de procesamiento de señales IEEE 34, 43–59 (2017).
https: / / doi.org/ 10.1109 / MSP.2017.2695801

[ 23 ] A. Gramfort, G. Peyré y M. Cuturi. “Promedio de transporte rápido y óptimo de datos de neuroimagen”. Procesamiento de Información en Imágenes Médicas. IPMI 2015. Apuntes de conferencias sobre informática 9123, 261–272 (2015).
https:/​/​doi.org/​10.1007/​978-3-319-19992-4_20

[ 24 ] Z. Su, W. Zeng, Y. Wang, ZL Lu y X. Gu. “Clasificación de formas mediante la distancia de Wasserstein para el análisis de morfometría cerebral”. Procesamiento de Información en Imágenes Médicas. IPMI 2015. Apuntes de conferencias sobre informática 24, 411–423 (2015).
https:/​/​doi.org/​10.1007/​978-3-319-19992-4_32

[ 25 ] Martin Arjovsky, Soumith Chintala y Léon Bottou. “Redes generativas adversarias de Wasserstein”. En Doina Precup y Yee Whye Teh, editores, Actas de la 34ª Conferencia Internacional sobre Aprendizaje Automático. Volumen 70 de Actas de investigación sobre aprendizaje automático, páginas 214–223. PMLR (2017). arXiv:1701.07875.
arXiv: 1701.07875

[ 26 ] TA El Moselhy y YM Marzouk. "Inferencia bayesiana con mapas óptimos". J. Computación. Física. 231, 7815–7850 (2012).
https: / / doi.org/ 10.1016 / j.jcp.2012.07.022

[ 27 ] Gabriel Peyré y Marco Cuturi. “Transporte óptimo computacional: con aplicaciones a la ciencia de datos”. Encontró. Aprendizaje automático de tendencias. 11, 355–602 (2019).
https: / / doi.org/ 10.1561 / 2200000073

[ 28 ] Charlie Frogner, Chiyuan Zhang, Hossein Mobahi, Mauricio Araya y Tomaso A Poggio. “Aprender con pérdida de Wasserstein”. En C. Cortes, N. Lawrence, D. Lee, M. Sugiyama y R. Garnett, editores, Advances in Neural Information Processing Systems. Volumen 28. Curran Associates, Inc. (2015). arXiv:1506.05439.
arXiv: 1506.05439

[ 29 ] A. Ramdas, NG Trillos y M. Cuturi. "Sobre las pruebas de dos muestras de Wasserstein y familias relacionadas de pruebas no paramétricas". Entropía 19, 47. (2017).
https: / / doi.org/ 10.3390 / e19020047

[ 30 ] S. Srivastava, C. Li y DB Dunson. "Bayes escalable a través de Barycenter en Wasserstein Space". J. Mach. Aprender. Res. 19, 1–35 (2018). arXiv:1508.05880.
arXiv: 1508.05880

[ 31 ] Karol Życzkowski y Wojeciech Slomczynski. “La distancia de Monge entre estados cuánticos”. J. Física. R: Matemáticas. Gen. 31, 9095–9104 (1998).
https:/​/​doi.org/​10.1088/​0305-4470/​31/​45/​009

[ 32 ] Karol Życzkowski y Wojciech Slomczynski. “La métrica de Monge sobre la esfera y geometría de los estados cuánticos”. J. Física. R: Matemáticas. Gen. 34, 6689–6722 (2001).
https:/​/​doi.org/​10.1088/​0305-4470/​34/​34/​311

[ 33 ] Ingemar Bengtsson y Karol Zyczkowski. “Geometría de estados cuánticos: una introducción al entrelazamiento cuántico”. Prensa de la Universidad de Cambridge. (2006).
https: / / doi.org/ 10.1017 / CBO9780511535048

[ 34 ] P. Biane y D. Voiculescu. "Un análogo de probabilidad libre de la métrica de Wasserstein en el espacio de estados de traza". GAFA, Geom. Función. Anal. 11, 1125-1138 (2001).
https:/​/​doi.org/​10.1007/​s00039-001-8226-4

[ 35 ] Eric A. Carlen y Jan Maas. "Un análogo de la métrica de 2-Wasserstein en probabilidad no conmutativa bajo la cual la ecuación fermiónica de Fokker-Planck es un flujo de gradiente para la entropía". Comunitario. Matemáticas. Física. 331, 887–926 (2014).
https:/​/​doi.org/​10.1007/​s00220-014-2124-8

[ 36 ] Eric A. Carlen y Jan Maas. “Desigualdades de flujo de gradiente y entropía para semigrupos cuánticos de Markov con equilibrio detallado”. J. Función. Anal. 273, 1810–1869 (2017).
https: / / doi.org/ 10.1016 / j.jfa.2017.05.003

[ 37 ] Eric A. Carlen y Jan Maas. “Cálculo no conmutativo, transporte óptimo y desigualdades funcionales en sistemas cuánticos disipativos”. J. estadística. Física. 178, 319–378 (2020).
https: / / doi.org/ 10.1007 / s10955-019-02434-w

[ 38 ] Nilanjana Datta y Cambyse Rouzé. “Concentración de estados cuánticos a partir de desigualdades cuánticas funcionales y de costos de transporte”. J. Matemáticas. Física. 60, 012202 (2019).
https: / / doi.org/ 10.1063 / 1.5023210

[ 39 ] Nilanjana Datta y Cambyse Rouzé. "Relacionando la entropía relativa, el transporte óptimo y la información de Fisher: una desigualdad cuántica de HWI". Ana. Henri Poincaré 21, 2115-2150 (2020).
https:/​/​doi.org/​10.1007/​s00023-020-00891-8

[ 40 ] François Golse, Clément Mouhot y Thierry Paul. “Sobre el campo medio y los límites clásicos de la mecánica cuántica”. Comunitario. Matemáticas. Física. 343, 165-205 (2016).
https:/​/​doi.org/​10.1007/​s00220-015-2485-7

[ 41 ] François Golse y Thierry Paul. “La ecuación de Schrödinger en el campo medio y régimen semiclásico”. Arco. Racionar. Mec. Anal. 223, 57–94 (2017).
https: / / doi.org/ 10.1007 / s00205-016-1031-x

[ 42 ] François Golse y Thierry Paul. “Paquetes de ondas y distancia cuadrática de Monge-Kantorovich en mecánica cuántica”. Cuentas Rendus Matemáticas. 356, 177-197 (2018).
https://​/​doi.org/​10.1016/​j.crma.2017.12.007

[ 43 ] François Golse. “El problema del cuerpo cuántico $N$ en el régimen semiclásico y de campo medio”. Fil. Trans. R. Soc. A 376, 20170229 (2018).
https: / / doi.org/ 10.1098 / rsta.2017.0229

[ 44 ] E. Caglioti, F. Golse y T. Paul. “El transporte cuántico óptimo es más barato”. J. estadística. Física. 181, 149-162 (2020).
https:/​/​doi.org/​10.1007/​s10955-020-02571-7

[ 45 ] Emanuele Caglioti, François Golse y Thierry Paul. “Hacia un transporte óptimo para densidades cuánticas”. arXiv:2101.03256 (2021).
https://​/​doi.org/​10.48550/​arXiv.2101.03256
arXiv: 2101.03256

[ 46 ] Giacomo De Palma y Darío Trevisan. “Transporte cuántico óptimo con canales cuánticos”. Ana. Henri Poincaré 22, 3199–3234 (2021).
https:/​/​doi.org/​10.1007/​s00023-021-01042-3

[ 47 ] Giacomo De Palma, Milad Marvian, Dario Trevisan y Seth Lloyd. "La distancia cuántica de Wasserstein de orden 1". Traducción IEEE. inf. Teoría 67, 6627–6643 (2021).
https: / / doi.org/ 10.1109 / TIT.2021.3076442

[ 48 ] Shmuel Friedland, Michał Eckstein, Sam Cole y Karol Życzkowski. “Problema cuántico de Monge-Kantorovich y distancia de transporte entre matrices de densidad”. Física. Rev. Lett. 129, 110402 (2022).
https: / / doi.org/ 10.1103 / PhysRevLett.129.110402

[ 49 ] Sam Cole, Michał Eckstein, Shmuel Friedland y Karol Życzkowski. “Transporte cuántico óptimo”. arXiv:2105.06922 (2021).
https://​/​doi.org/​10.48550/​arXiv.2105.06922
arXiv: 2105.06922

[ 50 ] R. Bistroń, M. Eckstein y K. Życzkowski. "Monotonicidad de una distancia cuántica de 2-Wasserstein". J. Física. R: Matemáticas. Teor. 56, 095301 (2023).
https:/​/​doi.org/​10.1088/​1751-8121/​acb9c8

[ 51 ] György Pál Gehér, József Pitrik, Tamás Titkos y Dániel Virosztek. "Isometrías cuánticas de Wasserstein en el espacio de estados de qubits". J. Matemáticas. Anal. Aplica. 522, 126955 (2023).
https://​/​doi.org/​10.1016/​j.jmaa.2022.126955

[ 52 ] Lu Li, Kaifeng Bu, Dax Enshan Koh, Arthur Jaffe y Seth Lloyd. "Complejidad de Wasserstein de los circuitos cuánticos". arXiv: 2208.06306 (2022).
https://​/​doi.org/​10.48550/​arXiv.2208.06306

[ 53 ] Bobak Toussi Kiani, Giacomo De Palma, Milad Marvian, Zi-Wen Liu y Seth Lloyd. “Aprendizaje de datos cuánticos con la distancia del motor cuántico de la Tierra”. Ciencia cuántica. Tecnología. 7, 045002 (2022).
https:/​/​doi.org/​10.1088/​2058-9565/​ac79c9

[ 54 ] EP Wigner y Mutsuo M. Yanase. “Contenidos informativos de las distribuciones”. Proc. Nacional. Acad. Ciencia. Estados Unidos 49, 910–918 (1963).
https: / / doi.org/ 10.1073 / pnas.49.6.910

[ 55 ] Ryszard Horodecki, Paweł Horodecki, Michał Horodecki y Karol Horodecki. "Entrelazamiento cuántico". Rev.Mod. física 81, 865–942 (2009).
https: / / doi.org/ 10.1103 / RevModPhys.81.865

[ 56 ] Otfried Gühne y Géza Tóth. “Detección de enredos”. física Rep. 474, 1–75 (2009).
https: / / doi.org/ 10.1016 / j.physrep.2009.02.004

[ 57 ] Nicolai Friis, Giuseppe Vitagliano, Mehul Malik y Marcus Huber. “Certificación de entrelazamiento de la teoría al experimento”. Nat. Rev. Phys. 1, 72–87 (2019).
https:/​/​doi.org/​10.1038/​s42254-018-0003-5

[ 58 ] Vittorio Giovannetti, Seth Lloyd y Lorenzo Maccone. "Mediciones mejoradas cuánticamente: superando el límite cuántico estándar". Ciencia 306, 1330–1336 (2004).
https: / / doi.org/ 10.1126 / science.1104149

[ 59 ] Matteo GA París. “Estimación cuántica para tecnología cuántica”. En t. J. Cuant. inf. 07, 125-137 (2009).
https: / / doi.org/ 10.1142 / S0219749909004839

[ 60 ] Rafal Demkowicz-Dobrzanski, Marcin Jarzyna y Jan Kolodynski. “Capítulo cuatro – Límites cuánticos en interferometría óptica”. Prog. Óptica 60, 345 – 435 (2015). arXiv:1405.7703.
https: / / doi.org/ 10.1016 / bs.po.2015.02.003
arXiv: 1405.7703

[ 61 ] Luca Pezze y Augusto Smerzi. “Teoría cuántica de la estimación de fases”. En GM Tino y MA Kasevich, editores, Interferometría atómica (Proc. Int. Escuela de Física 'Enrico Fermi', Curso 188, Varenna). Páginas 691–741. IOS Press, Ámsterdam (2014). arXiv:1411.5164.
arXiv: 1411.5164

[ 62 ] Géza Tóth y Dénes Petz. “Propiedades extremas de la varianza y la información cuántica de Fisher”. Física. Rev. A 87, 032324 (2013).
https: / / doi.org/ 10.1103 / PhysRevA.87.032324

[ 63 ] Sixia Yu. "La información de Quantum Fisher como techo convexo de varianza". arXiv:1302.5311 (2013).
https://​/​doi.org/​10.48550/​arXiv.1302.5311
arXiv: 1302.5311

[ 64 ] Géza Tóth y Florian Fröwis. “Relaciones de incertidumbre con la varianza y la información cuántica de Fisher basadas en descomposiciones convexas de matrices de densidad”. Física. Rev. Investigación 4, 013075 (2022).
https: / / doi.org/ 10.1103 / PhysRevResearch.4.013075

[ 65 ] Shao-Hen Chiew y Manuel Gessner. "Mejora de las relaciones de incertidumbre de la suma con la información cuántica de Fisher". Física. Rev. Investigación 4, 013076 (2022).
https: / / doi.org/ 10.1103 / PhysRevResearch.4.013076

[ 66 ] CW Helstrom. “Teoría de la detección y estimación cuántica”. Prensa académica, Nueva York. (1976). URL: www.elsevier.com/​books/​quantum-detection-and-estimation-theory/​helstrom/​978-0-12-340050-5.
https:/​/​www.elsevier.com/​books/​quantum-detection-and-estimation-theory/​helstrom/​978-0-12-340050-5

[ 67 ] AS Holevo. “Aspectos probabilísticos y estadísticos de la teoría cuántica”. Holanda Septentrional, Ámsterdam. (mil novecientos ochenta y dos).

[ 68 ] Samuel L. Braunstein y Carlton M. Cuevas. “Distancia estadística y geometría de estados cuánticos”. física Rev. Lett. 72, 3439–3443 (1994).
https: / / doi.org/ 10.1103 / PhysRevLett.72.3439

[ 69 ] Samuel L Braunstein, Carlton M Caves y Gerard J Milburn. “Relaciones de incertidumbre generalizada: teoría, ejemplos e invariancia de Lorentz”. Ana. Física. 247, 135-173 (1996).
https: / / doi.org/ 10.1006 / aphy.1996.0040

[ 70 ] Dénes Petz. “Teoría de la información cuántica y estadística cuántica”. Springer, Berlín, Heilderberg. (2008).
https:/​/​doi.org/​10.1007/​978-3-540-74636-2

[ 71 ] Géza Tóth y Iagoba Apellaniz. “Metrología cuántica desde la perspectiva de la ciencia de la información cuántica”. J. física. R: Matemáticas. teor. 47, 424006 (2014).
https:/​/​doi.org/​10.1088/​1751-8113/​47/​42/​424006

[ 72 ] Luca Pezzè, Augusto Smerzi, Markus K. Oberthaler, Roman Schmied y Philipp Treutlein. “Metrología cuántica con estados no clásicos de conjuntos atómicos”. Rev.Mod. física 90, 035005 (2018).
https: / / doi.org/ 10.1103 / RevModPhys.90.035005

[ 73 ] Marco Barbieri. “Metrología cuántica óptica”. PRX Cuántico 3, 010202 (2022).
https: / / doi.org/ 10.1103 / PRXQuantum.3.010202

[ 74 ] Zoltán Léka y Dénes Petz. “Algunas descomposiciones de varianzas matriciales”. Probablemente. Matemáticas. Estadístico. 33, 191-199 (2013). arXiv:1408.2707.
arXiv: 1408.2707

[ 75 ] Dénes Petz y Dániel Virosztek. "Un teorema de caracterización de varianzas matriciales". Acta de ciencia. Matemáticas. (Szeged) 80, 681–687 (2014).
https:/​/​doi.org/​10.14232/​actasm-013-789-z

[ 76 ] Akio Fujiwara e Hiroshi Imai. "Un haz de fibras sobre múltiples canales cuánticos y su aplicación a la estadística cuántica". J. Física. R: Matemáticas. Teor. 41, 255304 (2008).
https:/​/​doi.org/​10.1088/​1751-8113/​41/​25/​255304

[ 77 ] BM Escher, RL de Matos Filho y L. Davidovich. "Marco general para estimar el límite último de precisión en metrología ruidosa mejorada cuántica". Nat. Física. 7, 406–411 (2011).
https: / / doi.org/ 10.1038 / nphys1958

[ 78 ] Rafał Demkowicz-Dobrzański, Jan Kołodyński y Mădălin Guţă. "El elusivo límite de Heisenberg en metrología mejorada cuántica". Nat. Comunitario. 3, 1063 (2012).
https: / / doi.org/ 10.1038 / ncomms2067

[ 79 ] Imán Marvian. "Interpretación operativa de la información de Fisher cuántica en termodinámica cuántica". Física. Rev. Lett. 129, 190502 (2022).
https: / / doi.org/ 10.1103 / PhysRevLett.129.190502

[ 80 ] Reinhard F. Werner. “Estados cuánticos con correlaciones de Einstein-Podolsky-Rosen admitiendo un modelo de variable oculta”. Física. Rev. A 40, 4277–4281 (1989).
https: / / doi.org/ 10.1103 / PhysRevA.40.4277

[ 81 ] K. Eckert, J. Schliemann, D. Bruss y M. Lewenstein. “Correlaciones cuánticas en sistemas de partículas indistinguibles”. Ana. Física. 299, 88-127 (2002).
https: / / doi.org/ 10.1006 / aphy.2002.6268

[ 82 ] Tsubasa Ichikawa, Toshihiko Sasaki, Izumi Tsutsui y Nobuhiro Yonezawa. “Simetría de intercambio y entrelazamiento multipartito”. Física. Rev. A 78, 052105 (2008).
https: / / doi.org/ 10.1103 / PhysRevA.78.052105

[ 83 ] Pawel Horodecki. “Criterio de separabilidad y estados mixtos inseparables con transposición parcial positiva”. Física. Letón. A 232, 333–339 (1997).
https:/​/​doi.org/​10.1016/​S0375-9601(97)00416-7

[ 84 ] Asher Peres. “Criterio de separabilidad para matrices de densidad”. física Rev. Lett. 77, 1413–1415 (1996).
https: / / doi.org/ 10.1103 / PhysRevLett.77.1413

[ 85 ] Paweł Horodecki, Michał Horodecki y Ryszard Horodecki. “Se puede activar el enredo ligado”. Física. Rev. Lett. 82, 1056-1059 (1999).
https: / / doi.org/ 10.1103 / PhysRevLett.82.1056

[ 86 ] Géza Tóth y Tamás Vértesi. "Los estados cuánticos con transposición parcial positiva son útiles para la metrología". Física. Rev. Lett. 120, 020506 (2018).
https: / / doi.org/ 10.1103 / PhysRevLett.120.020506

[ 87 ] Scott Hill y William K. Wootters. “Enredo de un par de bits cuánticos”. Física. Rev. Lett. 78, 5022–5025 (1997).
https: / / doi.org/ 10.1103 / PhysRevLett.78.5022

[ 88 ] William K. Wootters. “Enredo de formación de un estado arbitrario de dos qubits”. física Rev. Lett. 80, 2245–2248 (1998).
https: / / doi.org/ 10.1103 / PhysRevLett.80.2245

[ 89 ] David P. DiVincenzo, Christopher A. Fuchs, Hideo Mabuchi, John A. Smolin, Ashish Thapliyal y Armin Uhlmann. “Enredo de asistencia”. cuanto-ph/​9803033 (1998).
https:/​/​doi.org/​10.48550/​arXiv.quant-ph/​9803033
arXiv: quant-ph / 9803033

[ 90 ] John A. Smolin, Frank Verstraete y Andreas Winter. “Enredo de asistencia y destilación estatal multipartidista”. Física. Rev. A 72, 052317 (2005).
https: / / doi.org/ 10.1103 / PhysRevA.72.052317

[ 91 ] Holger F. Hofmann y Shigeki Takeuchi. “La violación de las relaciones de incertidumbre local como firma del entrelazamiento”. Física. Rev. A 68, 032103 (2003).
https: / / doi.org/ 10.1103 / PhysRevA.68.032103

[ 92 ] Otfried Gühne. "Caracterización del entrelazamiento a través de relaciones de incertidumbre". Física. Rev. Lett. 92, 117903 (2004).
https: / / doi.org/ 10.1103 / PhysRevLett.92.117903

[ 93 ] Otfried Gühne, Mátyás Mechler, Géza Tóth y Peter Adam. "Los criterios de entrelazamiento basados ​​en relaciones de incertidumbre locales son estrictamente más fuertes que el criterio computable de normas cruzadas". Física. Rev. A 74, 010301 (2006).
https: / / doi.org/ 10.1103 / PhysRevA.74.010301

[ 94 ] Giuseppe Vitagliano, Philipp Hyllus, Iñigo L. Egusquiza y Géza Tóth. “Desigualdades de compresión de espín para espín arbitrario”. física Rev. Lett. 107, 240502 (2011).
https: / / doi.org/ 10.1103 / PhysRevLett.107.240502

[ 95 ] AR Edmonds. “Momento angular en mecánica cuántica”. Prensa de la Universidad de Princeton. (1957).
https: / / doi.org/ 10.1515 / 9781400884186

[ 96 ] Geza Toth. “Detección de entrelazamiento en redes ópticas de átomos bosónicos con medidas colectivas”. física Rev. A 69, 052327 (2004).
https: / / doi.org/ 10.1103 / PhysRevA.69.052327

[ 97 ] Géza Tóth, Christian Knapp, Otfried Gühne y Hans J. Briegel. "Las desigualdades óptimas de compresión de espín detectan enredos enlazados en modelos de espín". física Rev. Lett. 99, 250405 (2007).
https: / / doi.org/ 10.1103 / PhysRevLett.99.250405

[ 98 ] Géza Tóth y Morgan W Mitchell. “Generación de estados singlete macroscópicos en conjuntos atómicos”. Nuevo J. Phys. 12, 053007 (2010).
https:/​/​doi.org/​10.1088/​1367-2630/​12/​5/​053007

[ 99 ] Géza Tóth. "Detección de entrelazamiento multipartito en las proximidades de estados simétricos de Dicke". J. Optar. Soc. Soy. B 24, 275–282 (2007).
https: / / doi.org/ 10.1364 / JOSAB.24.000275

[ 100 ] Géza Tóth, Tobias Moroder y Otfried Gühne. “Evaluación de medidas de enredo de techos convexos”. Física. Rev. Lett. 114, 160501 (2015).
https: / / doi.org/ 10.1103 / PhysRevLett.114.160501

[ 101 ] Lieven Vandenberghe y Stephen Boyd. “Programación semidefinida”. Revisión SIAM 38, 49–95 (1996).
https: / / doi.org/ 10.1137 / 1038003

[ 102 ] Geza Toth. “Entrelazamiento multipartito y metrología de alta precisión”. física Rev. A 85, 022322 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.022322

[ 103 ] Philipp Hyllus, Wiesław Laskowski, Roland Krischek, Christian Schwemmer, Witlef Wieczorek, Harald Weinfurter, Luca Pezzé y Augusto Smerzi. “Información de Fisher y entrelazamiento de partículas múltiples”. física Rev. A 85, 022321 (2012).
https: / / doi.org/ 10.1103 / PhysRevA.85.022321

[ 104 ] Géza Tóth, Tamás Vértesi, Paweł Horodecki y Ryszard Horodecki. “Activando la utilidad metrológica oculta”. Física. Rev. Lett. 125, 020402 (2020).
https: / / doi.org/ 10.1103 / PhysRevLett.125.020402

[ 105 ] AC Doherty, Pablo A. Parrilo y Federico M. Spedalieri. “Distinguir estados separables y entrelazados”. Física. Rev. Lett. 88, 187904 (2002).
https: / / doi.org/ 10.1103 / PhysRevLett.88.187904

[ 106 ] Andrew C. Doherty, Pablo A. Parrilo y Federico M. Spedalieri. “Familia completa de criterios de separabilidad”. Física. Rev. A 69, 022308 (2004).
https: / / doi.org/ 10.1103 / PhysRevA.69.022308

[ 107 ] Andrew C. Doherty, Pablo A. Parrilo y Federico M. Spedalieri. "Detección de entrelazamiento multipartito". Física. Rev. A 71, 032333 (2005).
https: / / doi.org/ 10.1103 / PhysRevA.71.032333

[ 108 ] Harold Ollivier y Wojciech H. Zurek. “Discordancia cuántica: una medida de la cuantía de las correlaciones”. física Rev. Lett. 88, 017901 (2001).
https: / / doi.org/ 10.1103 / PhysRevLett.88.017901

[ 109 ] L. Henderson y V. Vedral. “Correlaciones clásicas, cuánticas y totales”. J. Física. R: Matemáticas. Génesis 34, 6899 (2001).
https:/​/​doi.org/​10.1088/​0305-4470/​34/​35/​315

[ 110 ] Anindita Bera, Tamoghna Das, Debasis Sadhukhan, Sudipto Singha Roy, Aditi Sen(De) y Ujjwal Sen. “La discordia cuántica y sus aliados: una revisión del progreso reciente”. Prog. Rep. Física. 81, 024001 (2017).
https: / / doi.org/ 10.1088 / 1361-6633 / aa872f

[ 111 ] Dénes Petz. “Covarianza e información de Fisher en mecánica cuántica”. J. Física. R: Matemáticas. Génesis 35, 929 (2002).
https:/​/​doi.org/​10.1088/​0305-4470/​35/​4/​305

[ 112 ] Paolo Gibilisco, Fumio Hiai y Dénes Petz. "Covarianza cuántica, información cuántica de Fisher y relaciones de incertidumbre". Traducción IEEE. inf. Teoría 55, 439–443 (2009).
https: / / doi.org/ 10.1109 / TIT.2008.2008142

[ 113 ] D. Petz y C. Ghinea. “Introducción a la información cuántica de Fisher”. Volumen 27, páginas 261–281. Científico mundial. (2011).
https: / / doi.org/ 10.1142 / 9789814338745_0015

[ 114 ] Frank Hansen. “Información de asimetría ajustada métrica”. Proc. Nacional. Acad. Ciencia. Estados Unidos 105, 9909–9916 (2008).
https: / / doi.org/ 10.1073 / pnas.0803323105

[ 115 ] Paolo Gibilisco, Davide Girolami y Frank Hansen. "Un enfoque unificado para la incertidumbre cuántica local y la potencia interferométrica mediante información de asimetría ajustada métricamente". Entropía 23, 263 (2021).
https: / / doi.org/ 10.3390 / e23030263

[ 116 ] MATLAB. “9.9.0.1524771(r2020b)”. MathWorks Inc. Natick, Massachusetts (2020).

[ 117 ] MOSEK ApS. “La caja de herramientas de optimización MOSEK para el manual de MATLAB. Versión 9.0”. (2019). URL: docs.mosek.com/​9.0/​toolbox/​index.html.
https://​/​docs.mosek.com/​9.0/​toolbox/​index.html

[ 118 ] J. Löfberg. “YALMIP: una caja de herramientas para modelado y optimización en MATLAB”. En Actas de la Conferencia CACSD. Taipei, Taiwán (2004).

[ 119 ] Géza Tóth. "QUBIT4MATLAB V3.0: Un paquete de programas para ciencia de la información cuántica y óptica cuántica para MATLAB". Computadora. Física. Comunitario. 179, 430–437 (2008).
https: / / doi.org/ 10.1016 / j.cpc.2008.03.007

[ 120 ] El paquete QUBIT4MATLAB está disponible en https:/​/​www.mathworks.com/​matlabcentral/​ fileexchange/​8433, y en la página de inicio personal https:/​/​gtoth.eu/​qubit4matlab.html.
https:/​/​www.mathworks.com/​matlabcentral/​fileexchange/​8433

Citado por

[1] Laurent Lafleche, “Transporte cuántico óptimo y topologías débiles”, arXiv: 2306.12944, (2023).

Las citas anteriores son de ANUNCIOS SAO / NASA (última actualización exitosa 2023-10-16 14:47:44). La lista puede estar incompleta ya que no todos los editores proporcionan datos de citas adecuados y completos.

No se pudo recuperar Crossref citado por datos durante el último intento 2023-10-16 14:47:42: No se pudieron obtener los datos citados por 10.22331 / q-2023-10-16-1143 de Crossref. Esto es normal si el DOI se registró recientemente.

Este documento se publica en Quantum bajo el Creative Commons Reconocimiento 4.0 Internacional (CC BY 4.0) licencia. Los derechos de autor permanecen con los titulares de derechos de autor originales, como los autores o sus instituciones.

Sello de tiempo:

Mas de Diario cuántico