Mayorización continua en el espacio de fase cuántica

Mayorización continua en el espacio de fase cuántica

Marca de tiempo: 24 de mayo de 2023 7:39 a.m.
Nodo de origen: 2674950

Zacharie Van Herstraeten1,2, Michael G. Jabbour1,3,4y Nicolás J. Cerf1

1Centro de Información y Comunicación Cuántica, École polytechnique de Bruxelles, CP 165/59, Université libre de Bruxelles, 1050 Bruselas, Bélgica
2Facultad de Ciencias Ópticas Wyant, Universidad de Arizona, 1630 E. University Blvd., Tucson, AZ 85721, EE. UU.
3DAMTP, Centro de Ciencias Matemáticas, Universidad de Cambridge, Cambridge CB3 0WA, Reino Unido
4Departamento de Física, Universidad Técnica de Dinamarca, 2800 Kongens Lyngby, Dinamarca

¿Encuentra este documento interesante o quiere discutirlo? Scite o deje un comentario en SciRate.

Resumen

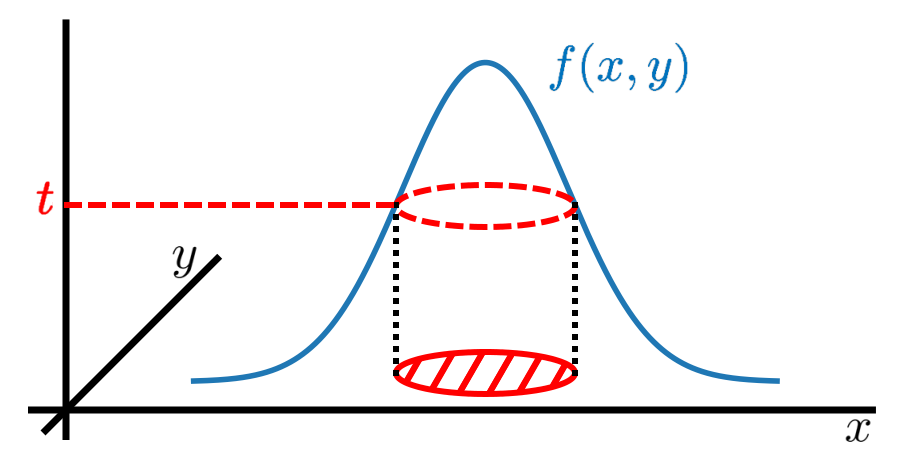
Exploramos el papel de la teoría de la mayorización en el espacio de fases cuánticas. Para ello, nos limitamos a estados cuánticos con funciones de Wigner positivas y mostramos que la versión continua de la teoría de la mayorización proporciona un enfoque elegante y muy natural para explorar las propiedades teóricas de la información de las funciones de Wigner en el espacio de fases. Después de identificar todos los estados puros gaussianos como equivalentes en el sentido preciso de mayorización continua, que puede entenderse a la luz del teorema de Hudson, conjeturamos una relación de mayorización fundamental: cualquier función de Wigner positiva es mayorizada por la función de Wigner de un estado puro gaussiano (especialmente , el estado de vacío bosónico o estado fundamental del oscilador armónico). Como consecuencia, cualquier función cóncava de Schur de la función de Wigner está limitada por el valor que toma para el estado de vacío. Esto implica, a su vez, que la entropía de Wigner está limitada por su valor para el estado de vacío, mientras que lo contrario no es cierto. Nuestro principal resultado es entonces demostrar esta relación de mayorización fundamental para un subconjunto relevante de estados cuánticos positivos de Wigner que son mezclas de los tres estados propios más bajos del oscilador armónico. Más allá de eso, la conjetura también está respaldada por evidencia numérica. Concluimos discutiendo algunas implicaciones de esta conjetura en el contexto de las relaciones de incertidumbre entrópica en el espacio de fases.

Resumen popular

El principio de incertidumbre es uno de los fenómenos más fascinantes de la física cuántica. Si bien puede parecer natural que pares de cantidades medibles, como la posición y el momento de una partícula, puedan predecirse simultáneamente con precisión, la física cuántica en realidad prohíbe esto para los observables que no conmutan. Heisenberg y Kennard precisaron esto empleando la varianza de cualquier cantidad medible para capturar su incertidumbre. Años más tarde, el principio de incertidumbre de Heisenberg fue reformulado recurriendo a la entropía como un medio adecuado para cuantificar la incertidumbre. Aquí, presentamos un paradigma teórico de la información aún más fuerte para comprender la incertidumbre de las variables cuánticas en el espacio de fase, a saber, la teoría de la mayorización.

Esta teoría matemática se desarrolló hace más de un siglo y se ha utilizado en numerosos campos de la ciencia, desde la estadística hasta la física. Sorprendentemente, se ha aplicado a la física cuántica hace relativamente poco tiempo, donde se demostró que es un enfoque poderoso para explorar el entrelazamiento cuántico. Como tal, nunca se ha explotado para caracterizar las densidades continuas que describen las variables cuánticas en el espacio de fase, es decir, las funciones de Wigner. Mostramos que la mayorización continua es una herramienta adecuada para esto. El objetivo principal de nuestro artículo se refiere a la afirmación de que la función de Wigner del estado de vacío de un modo bosónico (es decir, el estado fundamental del oscilador armónico) mayoriza continuamente a cualquier otra función de Wigner, haciéndola menos incierta en el sentido de mayorización. .

Si bien exponemos y discutimos nuestros resultados en el contexto de la óptica cuántica, se trasladan a cualquier par canónico y, por lo tanto, deberían tener implicaciones en varias áreas de la física.

► datos BibTeX

► referencias

[ 1 ] GH Hardy, JE Littlewood y G. Pólya, "Desigualdades". Prensa de la Universidad de Cambridge, 1934.
https: / / doi.org/ 10.2307 / 3605504

[ 2 ] AW Marshall, I. Olkin y BC Arnold, "Desigualdades: teoría de la mayorización y sus aplicaciones", vol. 143. Springer, segunda ed., 2011.
https:/​/​doi.org/​10.1007/​978-0-387-68276-1

[ 3 ] T. Ando, ​​``Mayorización, matrices doblemente estocásticas y comparación de valores propios'', Linear Algebra Appl. 118, 163–248 (1989).
https:/​/​doi.org/​10.1016/​0024-3795(89)90580-6

[ 4 ] K. Mosler, "Mayorización en medidas de disparidad económica", Linear Algebra and its Applications 199, 91-114 (1994).
https:/​/​doi.org/​10.1016/​0024-3795(94)90343-3

[ 5 ] T. van Erven y P. Harremoës, ``Rényi divergencia y mayorización'', en el Simposio internacional sobre teoría de la información del IEEE de 2010, págs. 1335-1339, IEEE. 2010.
https: / / doi.org/ 10.1109 / ISIT.2010.5513784

[ 6 ] MA Alhejji y G. Smith, "A Tight Uniform Continuity Bound for Equivocation", en el Simposio internacional sobre teoría de la información (ISIT) del IEEE de 2020, págs. 2270.
https: / / doi.org/ 10.1109 / ISIT44484.2020.9174350

[ 7 ] MG Jabbour y N. Datta, "Una continuidad uniforme estricta para la entropía condicional de Arimoto-Rényi y su extensión a los estados cuánticos clásicos", IEEE Transactions on Information Theory 68, 2169–2181 (2022).
https: / / doi.org/ 10.1109 / TIT.2022.3142812

[ 8 ] A. Horn, "Matrices doblemente estocásticas y la diagonal de una matriz de rotación", American Journal of Mathematics 76, 620–630 (1954).
https: / / doi.org/ 10.2307 / 2372705

[ 9 ] MA Nielsen, "Condiciones para una clase de transformaciones de entrelazamiento", Physical Review Letters 83, 436 (1999).
https: / / doi.org/ 10.1103 / PhysRevLett.83.436

[ 10 ] MA Nielsen y G. Vidal, "Mayorización y interconversión de estados bipartitos", Quantum Information and Computation 1, 76–93 (2001).
https: / / doi.org/ 10.26421 / QIC1.1-5

[ 11 ] MA Nielsen y J. Kempe, "Los estados separables están más desordenados globalmente que localmente", Physical Review Letters 86, 5184–5187 (2001).
https: / / doi.org/ 10.1103 / PhysRevLett.86.5184

[ 12 ] T. Hiroshima, "Criterio de mayorización para la destilabilidad de un estado cuántico bipartito", Physical Review Letters 91, 057902 (2003).
https: / / doi.org/ 10.1103 / PhysRevLett.91.057902

[ 13 ] Z. Puchała, Ł. Rudnicki y K. Życzkowski, "Relaciones de incertidumbre entrópica de mayorización", Journal of Physics A: Mathematical and Theoretical 46, 272002 (2013).
https:/​/​doi.org/​10.1088/​1751-8113/​46/​27/​272002

[ 14 ] L. Rudnicki, Z. Puchała y K. Życzkowski, ``Relaciones de incertidumbre entrópica de fuerte mayorización'', Physical Review A 89, 052115 (2014).
https: / / doi.org/ 10.1103 / PhysRevA.89.052115

[ 15 ] L. Rudnicki, "Enfoque de mayorización de las relaciones de incertidumbre entrópica para observables de grano grueso", Physical Review A 91, 032123 (2015).
https: / / doi.org/ 10.1103 / PhysRevA.91.032123

[ 16 ] F. Brandão, M. Horodecki, N. Ng, J. Oppenheim y S. Wehner, "Las segundas leyes de la termodinámica cuántica", Actas de la Academia Nacional de Ciencias 112, 3275–3279 (2015).
https: / / doi.org/ 10.1073 / pnas.1411728112

[ 17 ] R. García-Patrón, C. Navarrete-Benlloch, S. Lloyd, JH Shapiro y NJ Cerf, ``Enfoque de la teoría de la mayorización para la conjetura de entropía mínima del canal gaussiano'', Physical Review Letters 108, 110505 (2012).
https: / / doi.org/ 10.1103 / PhysRevLett.108.110505

[ 18 ] CN Gagatsos, O. Oreshkov y NJ Cerf, "Relaciones de mayorización y generación de entrelazamiento en un divisor de haz", Physical Review A 87, 042307 (2013).
https: / / doi.org/ 10.1103 / PhysRevA.87.042307

[ 19 ] G. De Palma, D. Trevisan y V. Giovannetti, "Los estados pasivos optimizan la salida de los canales cuánticos bosónicos gaussianos", IEEE Transactions on Information Theory 62, 2895–2906 (2016).
https: / / doi.org/ 10.1109 / TIT.2016.2547426

[ 20 ] MG Jabbour, R. García-Patrón y NJ Cerf, ``Preservación de la mayorización de canales bosónicos gaussianos'', New Journal of Physics 18, 073047 (2016).
https:/​/​doi.org/​10.1088/​1367-2630/​18/​7/​073047

[ 21 ] MG Jabbour y NJ Cerf, "Mayorización de Fock en canales cuánticos bosónicos con un entorno pasivo", Journal of Physics A: Mathematical and Theoretical 52, 105302 (2019).
https:/​/​doi.org/​10.1088/​1751-8121/​aaf0d2

[ 22 ] U. Leonhardt, "Óptica cuántica esencial: de las mediciones cuánticas a los agujeros negros". Prensa de la Universidad de Cambridge, 2010.
https: / / doi.org/ 10.1017 / CBO9780511806117

[ 23 ] A. Hertz, MG Jabbour y NJ Cerf, "Relaciones de incertidumbre entre entropía y poder: hacia una estrecha desigualdad para todos los estados puros gaussianos", Journal of Physics A: Mathematical and Theoretical 50, 385301 (2017).
https: / / doi.org/ 10.1088 / 1751-8121 / aa852f

[ 24 ] A. Hertz y NJ Cerf, "Relaciones de incertidumbre entrópica de variable continua", Journal of Physics A: Mathematical and Theoretical 52, 173001 (2019).
https:/​/​doi.org/​10.1088/​1751-8121/​ab03f3

[ 25 ] C. Weedbrook, S. Pirandola, R. García-Patrón, NJ Cerf, TC Ralph, JH Shapiro y S. Lloyd, "Información cuántica gaussiana", Review of Modern Physics 84, 621–669 (2012).
https: / / doi.org/ 10.1103 / RevModPhys.84.621

[ 26 ] Z. Van Herstraeten y NJ Cerf, "Entropía cuántica de Wigner", Physical Review A 104, 042211 (2021).
https: / / doi.org/ 10.1103 / PhysRevA.104.042211

[ 27 ] FJ Narcowich, ``Distribuciones de tipos y aplicaciones positivas de $hbar$'', Journal of mathphysics 30, 2565–2573 (1989).
https: / / doi.org/ 10.1063 / 1.528537

[ 28 ] T. Bröcker y R. Werner, "Estados mixtos con funciones de Wigner positivas", Revista de física matemática 36, ​​62–75 (1995).
https: / / doi.org/ 10.1063 / 1.531326

[ 29 ] RL Hudson, "¿Cuándo la densidad de cuasi probabilidad de Wigner no es negativa?", Reports on Mathematical Physics 6, 249-252 (1974).
https:/​/​doi.org/​10.1016/​0034-4877(74)90007-X

[ 30 ] F. Soto y P. Claverie, "¿Cuándo la función Wigner de los sistemas multidimensionales no es negativa?", Journal of Mathematical Physics 24, 97-100 (1983).
https: / / doi.org/ 10.1063 / 1.525607

[ 31 ] FJ Narcowich y R. O'Connell, "Condiciones necesarias y suficientes para que una función de espacio de fases sea una distribución de Wigner", Physical Review A 34, 1 (1986).
https: / / doi.org/ 10.1103 / PhysRevA.34.1

[ 32 ] A. Mandilara, E. Karpov y NJ Cerf, "Extensión del teorema de Hudson a estados cuánticos mixtos", Physical Review A 79, 062302 (2009).
https: / / doi.org/ 10.1103 / PhysRevA.79.062302

[ 33 ] A. Mandilara, E. Karpov y N. Cerf, "Límites de gaussianidad para estados mixtos cuánticos con una función de Wigner positiva", en Journal of Physics: Conference Series, vol. 254, pág. 012011, Publicación PIO. 2010.
https:/​/​doi.org/​10.1088/​1742-6596/​254/​1/​012011

[ 34 ] L. Wang y M. Madiman, "Más allá de la desigualdad del poder de la entropía, mediante reordenamientos", IEEE Transactions on Information Theory 60, 5116–5137 (2014).
https: / / doi.org/ 10.1109 / TIT.2014.2338852

[ 35 ] GH Hardy, JE Littlewood y G. Pólya, "Algunas desigualdades simples satisfechas por funciones convexas", Messenger of Mathematics 58, 145-152 (1929).

[ 36 ] H. Joe, "Un ordenamiento de dependencia para la distribución de k-tuplas, con aplicaciones a juegos de lotería", Canadian Journal of Statistics 15, 227-238 (1987).
https: / / doi.org/ 10.2307 / 3314913

[ 37 ] I. Schur, ``Uber eine Klasse von Mittelbildungen mit Anwendungen die Determinanten'', Sitzungsberichte der Berliner Mathematischen Gesellschaft 22, 416–427 (1923).

[ 38 ] AW Roberts y DE Varberg, "Funciones convexas". Prensa académica Nueva York, 1973.
https:/​/​doi.org/​10.1016/​B978-0-444-89597-4.50013-5

[ 39 ] A. Rényi, "Sobre medidas de entropía e información", en Actas del Cuarto Simposio de Berkeley sobre Estadística Matemática y Probabilidad, Volumen 1: Contribuciones a la Teoría de la Estadística, vol. 4, págs. 547–562, Prensa de la Universidad de California. 1961.

[ 40 ] Y. He, AB Hamza y H. Krim, "Una medida de divergencia generalizada para un registro de imágenes robusto", IEEE Transactions on Signal Processing 51, 1211-1220 (2003).
https://​/​doi.org/​10.1109/​TSP.2003.810305

[ 41 ] JV Ryff, ``Órbitas de funciones $L^1$ bajo transformaciones doblemente estocásticas'', Transactions of the American Mathematical Society 117, 92-100 (1965).
https: / / doi.org/ 10.2307 / 1994198

[ 42 ] F. Bahrami, SM Manjegani y S. Moein, "Operadores semidoblemente estocásticos y mayorización de funciones integrables", Boletín de la Sociedad de Ciencias Matemáticas de Malasia 44, 693–703 (2021).
https:/​/​doi.org/​10.1007/​s40840-020-00971-2

[ 43 ] SM Manjegani y S. Moein, ``Operadores de mayorización y semidoblemente estocásticos en $ L^{1}(X)$'', Journal of Inequalities and Applications 2023, 1–20 (2023).
https: / / doi.org/ 10.1186 / s13660-023-02935-z

[ 44 ] I. Białynicki-Birula y J. Mycielski, "Relaciones de incertidumbre para la entropía de la información en la mecánica ondulatoria", Communications in Mathematical Physics 44, 129-132 (1975).
https: / / doi.org/ 10.1007 / BF01608825

[ 45 ] A. Wehrl, "Propiedades generales de la entropía", Reviews of Modern Physics 50, 221 (1978).
https: / / doi.org/ 10.1103 / RevModPhys.50.221

[ 46 ] EH Lieb, "Prueba de una conjetura de entropía de Wehrl", en Desigualdades, págs. 359-365. Springer, 2002.
https:/​/​doi.org/​10.1007/​978-3-642-55925-9_30

[ 47 ] EH Lieb y JP Solovej, "Prueba de una conjetura de entropía para estados de espín coherentes de Bloch y sus generalizaciones", Acta Mathematica 212, 379 (2014).
https:/​/​doi.org/​10.1007/​s11511-014-0113-6

[ 48 ] JR Johansson, PD Nation y F. Nori, "QuTiP: un marco Python de código abierto para la dinámica de sistemas cuánticos abiertos", Computer Physics Communications 183, 1760–1772 (2012).
https: / / doi.org/ 10.1016 / j.cpc.2012.02.021

[ 49 ] K. Życzkowski, P. Horodecki, A. Sanpera y M. Lewenstein, "Volumen del conjunto de estados separables", Physical Review A 58, 883 (1998).
https: / / doi.org/ 10.1103 / PhysRevA.58.883

Citado por

[1] Nuno Costa Dias y João Nuno Prata, "Sobre una conjetura reciente de Z. Van Herstraeten y NJ Cerf para la entropía cuántica de Wigner", arXiv: 2303.10531, (2023).

[2] Zacharie Van Herstraeten y Nicolas J. Cerf, "Entropía cuántica de Wigner", Revisión física A 104 4, 042211 (2021).

[3] Martin Gärttner, Tobias Haas y Johannes Noll, "Detección de entrelazamiento variable continuo en el espacio de fases con la distribución $Q$", arXiv: 2211.17165, (2022).

Las citas anteriores son de ANUNCIOS SAO / NASA (última actualización exitosa 2023-05-24 23:55:18). La lista puede estar incompleta ya que no todos los editores proporcionan datos de citas adecuados y completos.

On Servicio de citaciones de Crossref no se encontraron datos sobre las obras citadas (último intento 2023-05-24 23:55:17).

Este documento se publica en Quantum bajo el Creative Commons Reconocimiento 4.0 Internacional (CC BY 4.0) licencia. Los derechos de autor permanecen con los titulares de derechos de autor originales, como los autores o sus instituciones.

Sello de tiempo:

Mas de Diario cuántico