Vitalik Buterin via Vitalik Buterin blog
Dette er et spejl af posten kl https://medium.com/@VitalikButerin/kvadratiske-aritmetiske-programmer-fra-nul-til-helt-f6d558cea649
Der har på det seneste været stor interesse for teknologien bag zk-SNARKs, og folk er i stigende grad forsøger at afmystificere noget, som mange er kommet til at kalde "månematematik" på grund af dets opfattede ren og skær uoverskuelige kompleksitet. zk-SNARK'er er faktisk ret udfordrende at forstå, især på grund af det store antal bevægelige dele, der skal samles for at det hele kan fungere, men hvis vi bryder teknologien ned stykke for stykke, bliver det nemmere at forstå det.
Formålet med dette indlæg er ikke at tjene som en fuldstændig introduktion til zk-SNARKs; det antager som baggrundsviden, at (i) du ved, hvad zk-SNARKs er, og hvad de gør, og (ii) kender nok matematik til at kunne ræsonnere om ting som polynomier (hvis udsagnet �(�)+�(�) =(�+�)(�) , hvor � og � er polynomier, virker naturligt og indlysende for dig, så er du på det rigtige niveau). Snarere graver indlægget dybere ned i maskineriet bag teknologien og forsøger så godt som muligt at forklare den første halvdel af pipelinen, som tegnet af zk-SNARK-forsker Eran Tromer her:

Trinene her kan deles op i to halvdele. For det første kan zk-SNARK'er ikke anvendes direkte på noget beregningsproblem; snarere skal du konvertere problemet til den rigtige "form", for at problemet kan opereres. Formen kaldes et "kvadratisk aritmetisk program" (QAP), og at transformere koden for en funktion til en af disse er i sig selv meget ikke-trivielt. Sammen med processen for at konvertere koden for en funktion til en QAP er en anden proces, der kan køres ved siden af, så hvis du har et input til koden, kan du oprette en tilsvarende løsning (nogle gange kaldet "vidne" til QAP). Herefter er der en anden ret indviklet proces til at skabe det faktiske "nulvidensbevis" for dette vidne, og en separat proces til at verificere et bevis for, at en anden videregiver til dig, men disse er detaljer, der er uden for dette indlægs rammer. .
Eksemplet, som vi vil vælge, er simpelt: at bevise, at du kender løsningen til en kubikligning: �3+�+5=35 (tip: svaret er 3). Dette problem er simpelt nok til, at den resulterende QAP ikke vil være så stor, at den er intimiderende, men ikke-triviel nok til, at du kan se alle maskineriet komme i spil.
Lad os skrive vores funktion ud som følger:
def qeval(x):
y = x**3
return x + y + 5Det enkle programmeringssprog, som vi bruger her, understøtter grundlæggende aritmetik (+, −, ⋅, /), eksponentiering med konstant effekt (�7 men ikke ��) og variabeltildeling, som er kraftfuld nok til, at du teoretisk kan udføre enhver beregning inde i den (så længe antallet af beregningstrin er begrænset; ingen sløjfer tilladt). Bemærk, at modulo (%) og sammenligningsoperatorer (<, >, ≤, ≥) IKKE er understøttet, da der ikke er nogen effektiv måde at udføre modulo eller sammenligning direkte i finite cyklisk gruppe aritmetik (vær taknemmelig for dette; hvis der var en måde for at udføre en af dem, ville elliptisk kurvekryptografi blive brudt hurtigere, end du kan sige "binær søgning" og "kinesisk restsætning").
Du kan udvide sproget til modulo og sammenligninger ved at levere bitdekomponeringer (f.eks. 13=23+22+1) som hjælpeindgange, bevise rigtigheden af disse dekomponeringer og lave matematikken i binære kredsløb; i finite field aritmetik er det også muligt at udføre lighedskontrol (==) og faktisk en smule lettere, men det er begge detaljer, vi ikke vil komme ind på lige nu. Vi kan udvide sproget til at understøtte betingelser (f.eks. hvis �<5:�=7; andet: �=9) ved at konvertere dem til en aritmetisk form: �=7⋅(�<5)+9⋅(�≥5) ) Bemærk dog, at begge "stier" af den betingede skal udføres, og hvis du har mange indlejrede betingede betingelser, kan dette føre til en stor mængde overhead.
Lad os nu gennemgå denne proces trin for trin. Hvis du ønsker at gøre dette selv for et stykke kode, I implementeret en compiler her (Kun til uddannelsesformål; ikke klar til at lave QAP'er til virkelige zk-SNARK'er endnu!).
Fladtrykthed
Det første trin er en "udfladningsprocedure", hvor vi konverterer den originale kode, som kan indeholde vilkårligt komplekse udsagn og udtryk, til en sekvens af udsagn, der har to former: �=� (hvor � kan være en variabel eller et tal ) og �=� (��) � (hvor �� kan være +, −, ⋅, / og � og � kan være variable, tal eller sig selv underudtryk). Du kan tænke på hver af disse udsagn som værende en slags logiske porte i et kredsløb. Resultatet af udfladningsprocessen for ovenstående kode er som følger:
sym_1 = x * x
y = sym_1 * x
sym_2 = y + x
~out = sym_2 + 5Hvis du læser den originale kode og koden her, kan du ret nemt se, at de to er ækvivalente.
Porte til R1CS
Nu konverterer vi dette til noget, der kaldes et rank-1 constraint system (R1CS). En R1CS er en sekvens af grupper af tre vektorer (�, �, �), og løsningen til en R1CS er en vektor �, hvor � skal opfylde ligningen �.�⋅�.�−�.�=0, hvor � . repræsenterer prikproduktet – i enklere vendinger, hvis vi "zipper sammen" � og �, multiplicerer de to værdier i de samme positioner, og derefter tager summen af disse produkter, gør du det samme med � og � og derefter � og � , så er det tredje resultat lig med produktet af de to første resultater. For eksempel er dette en tilfreds R1CS:
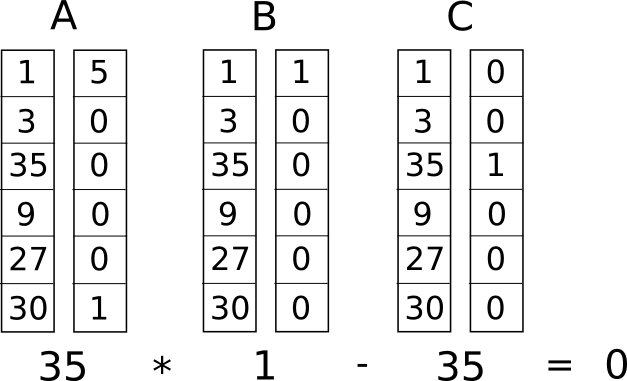
Men i stedet for kun at have én begrænsning, vil vi have mange begrænsninger: en for hver logisk port. Der er en standard måde at konvertere en logisk port til en (�,�,�) tripel afhængigt af, hvad operationen er (+, −, ⋅ eller /), og om argumenterne er variable eller tal. Længden af hver vektor er lig med det samlede antal variable i systemet, inklusive en dummy-variabel ~en ved det første indeks, der repræsenterer tallet 1, inputvariablerne, en dummy-variabel ~out, der repræsenterer output, og derefter alle mellemliggende variable (���1 og ���2 ovenfor); vektorerne vil generelt være meget sparsomme og kun udfylde de spalter, der svarer til de variable, der påvirkes af en bestemt logisk port.
Først giver vi den variabeltilknytning, som vi vil bruge:
'~one', 'x', '~out', 'sym_1', 'y', 'sym_2'Løsningsvektoren vil bestå af tildelinger for alle disse variable i nævnte rækkefølge.
Nu giver vi (�,�,�) tredobbelt for den første gate:
a = [0, 1, 0, 0, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 1, 0, 0]Du kan se, at hvis opløsningsvektoren indeholder 3 i den anden position og 9 i den fjerde position, så vil prikproduktkontrollen, uanset resten af indholdet af opløsningsvektoren, koge ned til 3⋅3=9, og så det går over. Hvis løsningsvektoren har −3 i den anden position og 9 i den fjerde position, vil kontrollen også bestå; faktisk, hvis løsningsvektoren har 7 i den anden position og 49 i den fjerde position, vil denne kontrol stadig passere - formålet med denne første kontrol er kun at verificere konsistensen af input og output fra den første port.
Lad os nu gå videre til den anden port:
a = [0, 0, 0, 1, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 0, 1, 0]I samme stil som det første punktprodukttjek, tjekker vi her, at ���1⋅�=�.
Nu, den tredje port:
a = [0, 1, 0, 0, 1, 0]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 0, 0, 0, 1]Her er mønsteret noget anderledes: det er at gange det første element i løsningsvektoren med det andet element, derefter med det femte element, tilføje de to resultater og kontrollere, om summen er lig med det sjette element. Fordi det første element i løsningsvektoren altid er ét, er dette blot en additionskontrol, der kontrollerer, at outputtet er lig med summen af de to input.
Til sidst den fjerde port:
a = [5, 0, 0, 0, 0, 1]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 1, 0, 0, 0]Her evaluerer vi den sidste check, ~out =���2+5. Punktproduktkontrollen fungerer ved at tage det sjette element i løsningsvektoren, tilføje fem gange det første element (påmindelse: det første element er 1, så det betyder i praksis, at man tilføjer 5), og tjekker det mod det tredje element, som er der, vi gemme outputvariablen.
Og der har vi vores R1CS med fire begrænsninger. Vidnet er simpelthen tildelingen til alle variablerne, inklusive input, output og interne variabler:
[1, 3, 35, 9, 27, 30]Du kan selv beregne dette ved blot at "udføre" den fladtrykte kode ovenfor, begynde med inputvariabeltildelingen �=3, og indsætte værdierne for alle de mellemliggende variabler og outputtet, mens du beregner dem.
Den komplette R1CS sammensat er:
A
[0, 1, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 0]
[0, 1, 0, 0, 1, 0]
[5, 0, 0, 0, 0, 1]
B
[0, 1, 0, 0, 0, 0]
[0, 1, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
C
[0, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 1, 0]
[0, 0, 0, 0, 0, 1]
[0, 0, 1, 0, 0, 0]R1CS til QAP
Det næste trin er at tage denne R1CS og konvertere den til QAP-form, som implementerer nøjagtig samme logik bortset fra at bruge polynomier i stedet for prikprodukter. Det gør vi som følger. Vi går 3fra fire grupper af tre vektorer af længden seks til seks grupper af tre grader-3 polynomier, hvor vi evaluerer polynomierne ved hver x koordinat repræsenterer en af begrænsningerne. Det vil sige, hvis vi vurderer polynomierne ved �=1, så får vi vores første sæt af vektorer, hvis vi evaluerer polynomierne ved �=2, så får vi vores andet sæt vektorer, og så videre.
Vi kan lave denne transformation ved at bruge noget, der hedder a Lagrange interpolation. Problemet, som en Lagrange-interpolation løser, er dette: Hvis du har et sæt punkter (dvs. (�,�) koordinatpar), så giver en Lagrange-interpolation på disse punkter dig et polynomium, der passerer gennem alle disse punkter. Vi gør dette ved at dekomponere problemet: For hver � koordinat opretter vi et polynomium, der har den ønskede � koordinat ved den � koordinat og en � koordinat på 0 ved alle de andre � koordinater, vi er interesserede i, og derefter for at få den endelige resultat lægger vi alle polynomier sammen.
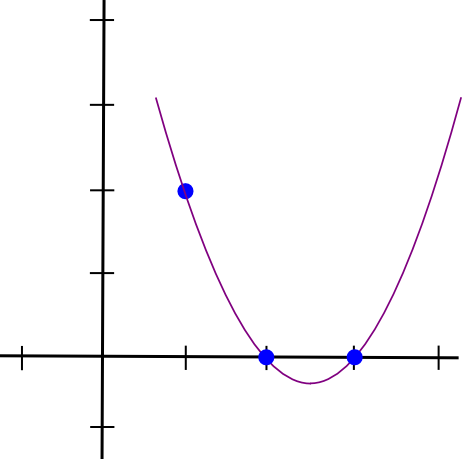
Lad os tage et eksempel. Antag, at vi ønsker et polynomium, der går gennem (1,3),(2,2) og (3,4). Vi starter med at lave et polynomium, der går gennem (1,3),(2,0) og (3,0). Som det viser sig, er det nemt at lave et polynomium, der "stikker ud" ved �=1 og er nul ved de andre interessepunkter; vi gør blot:
(x - 2) * (x - 3)Som ser sådan ud:
Nu skal vi bare "omskalere" det, så højden ved x=1 er rigtig:
(x - 2) * (x - 3) * 3 / ((1 - 2) * (1 - 3))Dette giver os:
1.5 * x**2 - 7.5 * x + 9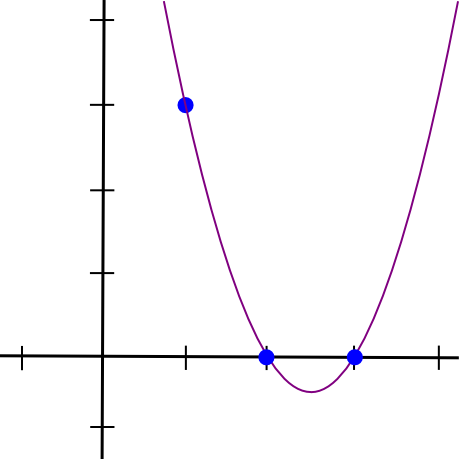
Vi gør så det samme med de to andre punkter og får to andre polynomier, der ligner hinanden, bortset fra at de "stikker ud" ved �=2 og �=3 i stedet for �=1. Vi lægger alle tre sammen og får:
1.5 * x**2 - 5.5 * x + 7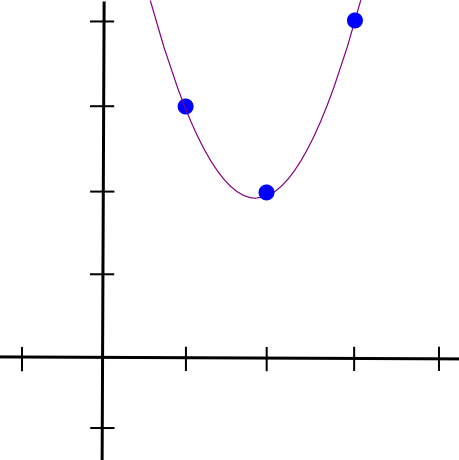
Med præcis de koordinater, som vi ønsker. Algoritmen som beskrevet ovenfor tager �(�3) tid, da der er � punkter, og hvert punkt kræver �(�2) tid til at gange polynomierne sammen; med lidt tænkning kan dette reduceres til �(�2) tid, og med meget mere tænkning, ved hjælp af hurtige Fourier-transformationsalgoritmer og lignende, kan det reduceres yderligere - en afgørende optimering, når funktioner, der bliver brugt i zk -SNARK'er har i praksis ofte mange tusinde porte.
Lad os nu bruge Lagrange-interpolation til at transformere vores R1CS. Det, vi skal gøre, er at tage den første værdi ud af hver � vektor, bruge Lagrange-interpolation til at lave et polynomium ud af det (hvor evaluering af polynomiet ved � giver dig den første værdi af den �th � vektor), gentag processen for den første værdi af hver � og � vektor, og gentag derefter denne proces for den anden værdi, den tredje, værdier og så videre. For nemheds skyld giver jeg svarene lige nu:
A polynomials
[-5.0, 9.166, -5.0, 0.833]
[8.0, -11.333, 5.0, -0.666]
[0.0, 0.0, 0.0, 0.0]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]
[-1.0, 1.833, -1.0, 0.166]
B polynomials
[3.0, -5.166, 2.5, -0.333]
[-2.0, 5.166, -2.5, 0.333]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
C polynomials
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[-1.0, 1.833, -1.0, 0.166]
[4.0, -4.333, 1.5, -0.166]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]Koefficienter er i stigende rækkefølge, så det første polynomium ovenfor er faktisk 0.833⋅�3—5⋅�2+9.166⋅�−5. Dette sæt polynomier (plus et Z-polynomium, som jeg vil forklare senere) udgør parametrene for denne særlige QAP-instans. Bemærk, at alt arbejdet indtil dette tidspunkt kun skal udføres én gang for hver funktion, som du forsøger at bruge zk-SNARKs til at verificere; når først QAP-parametrene er genereret, kan de genbruges.
Lad os prøve at evaluere alle disse polynomier ved �=1. At evaluere et polynomium ved �=1 betyder simpelthen at lægge alle koefficienterne sammen (som 1�=1 for alle �), så det er ikke svært. Vi får:
A results at x=1
0
1
0
0
0
0
B results at x=1
0
1
0
0
0
0
C results at x=1
0
0
0
1
0
0Og se, hvad vi har her er nøjagtig det samme som sættet af tre vektorer for den første logiske port, som vi skabte ovenfor.
Kontrollerer QAP
Hvad er nu meningen med denne skøre transformation? Svaret er, at i stedet for at kontrollere begrænsningerne i R1CS individuelt, kan vi nu tjekke alle begrænsningerne på samme tid ved at udføre prikkens produktcheck på polynomierne.
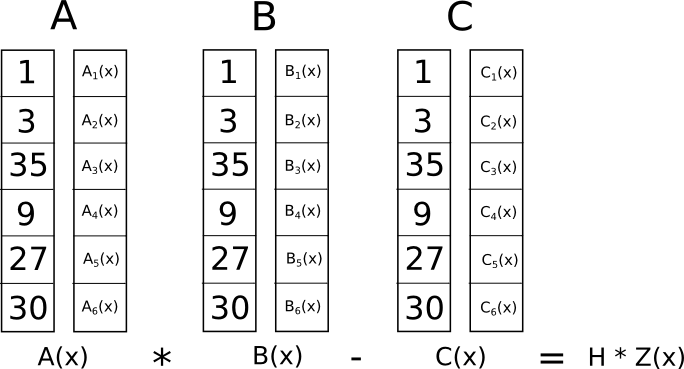
Fordi i dette tilfælde er prikproduktkontrollen en række additioner og multiplikationer af polynomier, vil resultatet i sig selv være et polynomium. Hvis det resulterende polynomium, evalueret ved hver � koordinat, som vi brugte ovenfor til at repræsentere en logisk port, er lig med nul, så betyder det, at alle kontrollerne består; hvis det resulterende polynomium evalueret ved mindst én af koordinaterne, der repræsenterer en logisk port, giver en værdi, der ikke er nul, betyder det, at værdierne, der går ind og ud af den logiske port, er inkonsistente (dvs. porten er �=�⋅�� �1, men de angivne værdier kan være �=2,���1=2 og �=5).
Bemærk, at det resulterende polynomium ikke i sig selv behøver at være nul, og i de fleste tilfælde vil det faktisk ikke være det; det kunne have en hvilken som helst adfærd på de punkter, der ikke svarer til nogen logiske porte, så længe resultatet er nul ved alle de punkter, der do svarer til en eller anden port. For at kontrollere rigtigheden evaluerer vi faktisk ikke polynomiet �=�.�⋅�.�−�.� ved hvert punkt, der svarer til en port; i stedet dividerer vi � med et andet polynomium, �, og kontrollerer, at � jævnt dividerer � – det vil sige, at divisionen �/� ikke efterlader nogen rest.
� er defineret som (�−1)⋅(�−2)⋅(�−3)... – det enkleste polynomium, der er lig med nul i alle punkter, der svarer til logiske porte. Det er et elementært faktum i algebra, at enhver polynomium, der er lig med nul ved alle disse punkter, skal være et multiplum af dette minimale polynomium, og hvis et polynomium er et multiplum af �, vil dets evaluering ved et hvilket som helst af disse punkter være nul; denne ækvivalens gør vores arbejde meget lettere.
Lad os nu faktisk foretage prikproduktkontrollen med polynomierne ovenfor. Først de mellemliggende polynomier:
A . s = [43.0, -73.333, 38.5, -5.166]
B . s = [-3.0, 10.333, -5.0, 0.666]
C . s = [-41.0, 71.666, -24.5, 2.833]Nu, �.�⋅�.�—�.�:
t = [-88.0, 592.666, -1063.777, 805.833, -294.777, 51.5, -3.444]Nu, det minimale polynomium �=(�−1)⋅(�−2)⋅(�−3)⋅(�−4):
Z = [24, -50, 35, -10, 1]Og hvis vi dividerer resultatet ovenfor med �, får vi:
h = t / Z = [-3.666, 17.055, -3.444]Uden rest.
Og så har vi løsningen til QAP. Hvis vi forsøger at forfalske en af variablerne i R1CS-løsningen, som vi udleder denne QAP-løsning fra - f.eks. sæt den sidste til 31 i stedet for 30, så får vi et � polynomium, der ikke består en af kontrollerne (i det særlige tilfælde, ville resultatet ved �=3 være lig med −1 i stedet for 0), og desuden ville � ikke være et multiplum af �; at dividere �/� ville snarere give en rest på [−5.0,8.833,−4.5,0.666].
Bemærk, at ovenstående er en forenkling; "i den virkelige verden", vil addition, multiplikation, subtraktion og division ikke ske med regulære tal, men snarere med endelige feltelementer - en uhyggelig form for aritmetik, som er selvkonsistent, så alle de algebraiske love, vi kender og elsker, stadig holder sandt, men hvor alle svar er elementer i en eller anden mængde af begrænset størrelse, normalt heltal inden for området fra 0 til �−1 for nogle �. For eksempel, hvis �=13, så 1/2=7 (og 7⋅2=1),3⋅5=2, og så videre. Brug af finite field aritmetik fjerner behovet for at bekymre sig om afrundingsfejl og giver systemet mulighed for at arbejde pænt med elliptiske kurver, som ender med at være nødvendige for resten af zk-SNARK maskineriet, der gør zk-SNARK protokollen faktisk sikker.
En særlig tak til Eran Tromer for at hjælpe mig med at forklare mange detaljer om zk-SNARKs indre virkemåde for mig.
- SEO Powered Content & PR Distribution. Bliv forstærket i dag.
- PlatoData.Network Vertical Generative Ai. Styrk dig selv. Adgang her.
- PlatoAiStream. Web3 intelligens. Viden forstærket. Adgang her.
- PlatoESG. Kulstof, CleanTech, Energi, Miljø, Solenergi, Affaldshåndtering. Adgang her.
- PlatoHealth. Bioteknologiske og kliniske forsøgs intelligens. Adgang her.
- BlockOffsets. Modernisering af miljømæssig offset-ejerskab. Adgang her.
- Kilde: Platon Data Intelligence.
