[মিরর] দ্বিঘাত পাটিগণিত প্রোগ্রাম: জিরো থেকে হিরো পর্যন্ত

ভিটালিক বুটেরিন এর মাধ্যমে ভিটালিক বুটেরিন ব্লগ

এটি এ পোস্টের একটি আয়না https://medium.com/@VitalikButerin/চতুর্ভুজ-পাটিগণিত-প্রোগ্রাম-থেকে-শূন্য-থেকে-নায়ক-f6d558cea649

zk-SNARK-এর পিছনে প্রযুক্তিতে ইদানীং প্রচুর আগ্রহ দেখা দিয়েছে এবং মানুষ ক্রমশ রহস্যময় করার চেষ্টা করছে এমন কিছু যাকে অনেকে "চাঁদের গণিত" বলে এসেছেন এর অনুভূত নিছক দুর্বোধ্য জটিলতার কারণে। zk-SNARK গুলি উপলব্ধি করা আসলেই বেশ চ্যালেঞ্জিং, বিশেষ করে চলমান অংশগুলির নিছক সংখ্যার কারণে যেগুলি পুরো জিনিসটি কাজ করার জন্য একত্রিত হওয়া দরকার, তবে আমরা যদি প্রযুক্তিটিকে টুকরো টুকরো করে ভেঙে ফেলি তবে এটি বোঝা সহজ হয়ে যায়।

এই পোস্টের উদ্দেশ্য zk-SNARK-এর সম্পূর্ণ পরিচিতি হিসাবে পরিবেশন করা নয়; এটি পটভূমির জ্ঞান হিসাবে ধরে নেয় যে (i) আপনি জানেন zk-SNARKগুলি কী এবং তারা কী করে এবং (ii) বহুপদগুলির মতো জিনিসগুলি সম্পর্কে যুক্তি দিতে সক্ষম হওয়ার জন্য যথেষ্ট গণিত জানেন (যদি বিবৃতি �(�)+�(�) =(�+�)(�), যেখানে � এবং � বহুপদ, আপনার কাছে স্বাভাবিক এবং সুস্পষ্ট বলে মনে হয়, তাহলে আপনি সঠিক স্তরে আছেন)। বরং, পোস্টটি প্রযুক্তির পিছনে থাকা যন্ত্রপাতিগুলির গভীরে খনন করে, এবং পাইপলাইনের প্রথমার্ধটি যতটা সম্ভব ব্যাখ্যা করার চেষ্টা করে, যেমনটি zk-SNARK গবেষক ইরান ট্রোমার এখানে আঁকেন:

এখানে পদক্ষেপ দুটি ভাগে বিভক্ত করা যেতে পারে। প্রথমত, zk-SNARK সরাসরি কোনো গণনাগত সমস্যায় প্রয়োগ করা যাবে না; বরং, সমস্যাটি চালু করার জন্য আপনাকে সমস্যাটিকে সঠিক "ফর্মে" রূপান্তর করতে হবে। ফর্মটিকে "চতুর্মুখী গাণিতিক প্রোগ্রাম" (QAP) বলা হয় এবং একটি ফাংশনের কোডকে এর মধ্যে একটিতে রূপান্তর করা নিজেই অত্যন্ত অতুচ্ছ। একটি ফাংশনের কোডকে একটি QAP-এ রূপান্তর করার প্রক্রিয়ার পাশাপাশি আরেকটি প্রক্রিয়া যা পাশাপাশি চালানো যেতে পারে যাতে আপনার যদি কোডটিতে একটি ইনপুট থাকে তবে আপনি একটি সংশ্লিষ্ট সমাধান তৈরি করতে পারেন (কখনও কখনও QAP-তে "সাক্ষী" বলা হয়)। এর পরে, এই সাক্ষীর জন্য প্রকৃত "জিরো নলেজ প্রুফ" তৈরি করার জন্য আরেকটি মোটামুটি জটিল প্রক্রিয়া আছে, এবং অন্য কেউ আপনার সাথে চলে গেছে এমন একটি প্রমাণ যাচাই করার জন্য একটি পৃথক প্রক্রিয়া, কিন্তু এই বিবরণগুলি এই পোস্টের সুযোগের বাইরে। .

আমরা যে উদাহরণটি বেছে নেব তা হল একটি সাধারণ: প্রমাণ করা যে আপনি একটি ঘন সমীকরণের সমাধান জানেন: �3+�+5=35 (ইঙ্গিত: উত্তরটি 3)। এই সমস্যাটি যথেষ্ট সহজ যে ফলাফল প্রাপ্ত QAP এত বড় হবে না যে ভয় দেখানো হবে, কিন্তু যথেষ্ট অতুচ্ছ যে আপনি দেখতে পাচ্ছেন যে সমস্ত যন্ত্রপাতি কার্যকর হয়ে আসছে।

আমাদের ফাংশনটি নিম্নরূপ লিখুন:

def qeval(x):
    y = x**3
    return x + y + 5

আমরা এখানে যে সাধারণ বিশেষ-উদ্দেশ্যের প্রোগ্রামিং ভাষা ব্যবহার করছি তা মৌলিক গাণিতিক (+, −, ⋅, /), ধ্রুব-শক্তি সূচক (�7 কিন্তু �� নয়) এবং পরিবর্তনশীল অ্যাসাইনমেন্ট সমর্থন করে, যা যথেষ্ট শক্তিশালী যে আপনি তাত্ত্বিকভাবে করতে পারেন। এর ভিতরে যেকোন গণনা (যতক্ষণ গণনামূলক পদক্ষেপের সংখ্যা আবদ্ধ থাকে; কোন লুপ অনুমোদিত নয়)। নোট করুন যে মডুলো (%) এবং তুলনা অপারেটর (<, >, ≤, ≥) সমর্থিত নয়, কারণ সরাসরি সসীম চক্রীয় গোষ্ঠীর গাণিতিকগুলিতে মডুলো বা তুলনা করার কোনও কার্যকর উপায় নেই (এর জন্য কৃতজ্ঞ থাকুন; যদি একটি উপায় থাকে যেকোনো একটি করতে, তাহলে উপবৃত্তাকার বক্ররেখা ক্রিপ্টোগ্রাফি আপনি "বাইনারী অনুসন্ধান" এবং "চীনা অবশিষ্ট উপপাদ্য" বলতে পারেন তার চেয়ে দ্রুত ভাঙা হবে)।

আপনি অক্জিলিয়ারী ইনপুট হিসাবে বিট পচন (যেমন 13=23+22+1) প্রদান করে, সেই পচনগুলির সঠিকতা প্রমাণ করে এবং বাইনারি সার্কিটে গণিত করার মাধ্যমে ভাষাটিকে মডিউল এবং তুলনাতে প্রসারিত করতে পারেন; সীমিত ক্ষেত্রের পাটিগণিতের মধ্যে, সমতা (==) চেক করাও সম্ভব এবং আসলে একটু সহজ, কিন্তু এই দুটি বিবরণ আমরা এখনই পাব না। আমরা শর্তাবলী সমর্থন করার জন্য ভাষাকে প্রসারিত করতে পারি (যেমন �<5:�=7; অন্য: �=9) একটি গাণিতিক ফর্মে রূপান্তর করে: �=7⋅(�<5)+9⋅(�≥5) ) যদিও মনে রাখবেন যে কন্ডিশনালের উভয় "পাথ" কার্যকর করা দরকার, এবং যদি আপনার অনেক নেস্টেড কন্ডিশনাল থাকে তবে এটি প্রচুর পরিমাণে ওভারহেডের দিকে নিয়ে যেতে পারে।

আসুন এখন ধাপে ধাপে এই প্রক্রিয়াটির মধ্য দিয়ে যাই। আপনি যদি কোডের যেকোনো অংশের জন্য এটি নিজে করতে চান, আমি এখানে একটি কম্পাইলার প্রয়োগ করা হয়েছে (শুধুমাত্র শিক্ষাগত উদ্দেশ্যে; বাস্তব-বিশ্বের zk-SNARK-এর জন্য QAP তৈরির জন্য এখনও প্রস্তুত নয়!)

সমরূপতার

প্রথম ধাপ হল একটি "চ্যাপ্টা" পদ্ধতি, যেখানে আমরা মূল কোডকে রূপান্তর করি, যার মধ্যে ইচ্ছাকৃতভাবে জটিল বিবৃতি এবং অভিব্যক্তি থাকতে পারে, বিবৃতিগুলির একটি ক্রমানুসারে যা দুটি রূপের: �=� (যেখানে � একটি পরিবর্তনশীল বা একটি সংখ্যা হতে পারে ) এবং �=� (��) � (যেখানে �� +, −, ⋅, / এবং � এবং � ভেরিয়েবল, সংখ্যা বা নিজেদের সাব-অভিব্যক্তি হতে পারে)। আপনি এই বিবৃতিগুলির প্রতিটিকে সার্কিটের লজিক গেটগুলির মতো মনে করতে পারেন। উপরের কোডের জন্য সমতল প্রক্রিয়ার ফলাফল নিম্নরূপ:

sym_1 = x * x
y = sym_1 * x
sym_2 = y + x
~out = sym_2 + 5

আপনি যদি মূল কোড এবং এখানে কোডটি পড়েন, আপনি মোটামুটি সহজেই দেখতে পাবেন যে দুটি সমতুল্য।

R1CS এর গেটস

এখন, আমরা এটিকে র‌্যাঙ্ক-1 কন্সট্রাইন্ট সিস্টেম (R1CS) নামক কিছুতে রূপান্তর করি। একটি R1CS হল তিনটি ভেক্টরের (�, �, �) গোষ্ঠীর একটি ক্রম এবং একটি R1CS-এর সমাধান হল একটি ভেক্টর �, যেখানে � অবশ্যই �.�⋅�.�−�.�=0, সমীকরণটি পূরণ করতে হবে . ডট পণ্যের প্রতিনিধিত্ব করে - সহজ ভাষায়, যদি আমরা "একসাথে জিপ" � এবং �, একই অবস্থানে দুটি মানকে গুণ করি এবং তারপর এই পণ্যগুলির যোগফল গ্রহণ করি, তাহলে � এবং � এবং তারপর � এবং � এর সাথে একই কাজ করি। , তারপর তৃতীয় ফলাফলটি প্রথম দুটি ফলাফলের গুণফলের সমান। উদাহরণস্বরূপ, এটি একটি সন্তুষ্ট R1CS:

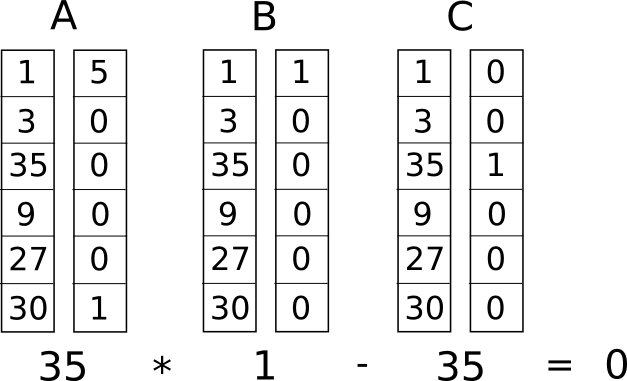
কিন্তু শুধুমাত্র একটি সীমাবদ্ধতার পরিবর্তে, আমাদের অনেক সীমাবদ্ধতা থাকবে: প্রতিটি লজিক গেটের জন্য একটি। একটি লজিক গেটকে একটি (�,�,�) ট্রিপলে রূপান্তর করার একটি আদর্শ উপায় রয়েছে যা অপারেশনটি কী (+, −, ⋅ বা /) এবং আর্গুমেন্টগুলি ভেরিয়েবল বা সংখ্যা কিনা তার উপর নির্ভর করে। প্রতিটি ভেক্টরের দৈর্ঘ্য সিস্টেমের মোট ভেরিয়েবলের সমান, যার মধ্যে একটি ডামি ভেরিয়েবল ~একটি প্রথম সূচকে 1 নম্বর, ইনপুট ভেরিয়েবল, একটি ডামি ভেরিয়েবল ~আউট যা আউটপুটকে প্রতিনিধিত্ব করে এবং তারপরে সমস্ত মধ্যবর্তী ভেরিয়েবল (উপরে ���1 এবং ���2); ভেক্টরগুলি সাধারণত খুব বিরল হতে চলেছে, শুধুমাত্র কিছু নির্দিষ্ট লজিক গেট দ্বারা প্রভাবিত ভেরিয়েবলের সাথে সম্পর্কিত স্লটগুলি পূরণ করা হয়।

প্রথমত, আমরা ভেরিয়েবল ম্যাপিং প্রদান করব যা আমরা ব্যবহার করব:

'~one', 'x', '~out', 'sym_1', 'y', 'sym_2'

সমাধান ভেক্টর এই সব ভেরিয়েবলের জন্য অ্যাসাইনমেন্ট নিয়ে গঠিত হবে, সেই ক্রমে।

এখন, আমরা প্রথম গেটের জন্য (�,�,�) ট্রিপল দেব:

a = [0, 1, 0, 0, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 1, 0, 0]

আপনি দেখতে পাচ্ছেন যে সমাধান ভেক্টরে যদি দ্বিতীয় অবস্থানে 3 এবং চতুর্থ অবস্থানে 9 থাকে, তাহলে সমাধান ভেক্টরের বাকি বিষয়বস্তু নির্বিশেষে, ডট পণ্য চেক 3⋅3=9 এ ফুটে উঠবে এবং তাই এটি পাস হবে। সমাধান ভেক্টরের দ্বিতীয় অবস্থানে −3 এবং চতুর্থ অবস্থানে 9 থাকলে, চেকটিও পাস হবে; প্রকৃতপক্ষে, যদি সমাধান ভেক্টরের দ্বিতীয় অবস্থানে 7 এবং চতুর্থ অবস্থানে 49 থাকে তবে সেই চেকটি এখনও পাস হবে — এই প্রথম চেকের উদ্দেশ্য শুধুমাত্র প্রথম গেটের ইনপুট এবং আউটপুটগুলির সামঞ্জস্য যাচাই করা।

এখন, দ্বিতীয় গেটে যাওয়া যাক:

a = [0, 0, 0, 1, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 0, 1, 0]

প্রথম ডট প্রোডাক্ট চেকের অনুরূপ শৈলীতে, এখানে আমরা এটি পরীক্ষা করছি ���1⋅�=�।

এখন, তৃতীয় গেট:

a = [0, 1, 0, 0, 1, 0]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 0, 0, 0, 1]

এখানে, প্যাটার্নটি কিছুটা ভিন্ন: এটি সমাধান ভেক্টরের প্রথম উপাদানটিকে দ্বিতীয় উপাদান দ্বারা গুণ করছে, তারপর পঞ্চম উপাদান দ্বারা, দুটি ফলাফল যোগ করছে এবং সমষ্টিটি ষষ্ঠ উপাদানের সমান কিনা তা পরীক্ষা করছে। কারণ সমাধান ভেক্টরের প্রথম উপাদানটি সর্বদা একটি, এটি শুধুমাত্র একটি সংযোজন চেক, আউটপুট দুটি ইনপুটের যোগফলের সমান কিনা তা পরীক্ষা করে।

অবশেষে, চতুর্থ গেট:

a = [5, 0, 0, 0, 0, 1]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 1, 0, 0, 0]

এখানে, আমরা শেষ চেকটি মূল্যায়ন করছি, ~out =���2+5। ডট প্রোডাক্ট চেক কাজ করে সমাধান ভেক্টরের ষষ্ঠ উপাদানটি নিয়ে, প্রথম উপাদানের পাঁচগুণ যোগ করে (অনুস্মারক: প্রথম উপাদানটি 1, তাই এর কার্যকরী অর্থ হল 5 যোগ করা), এবং তৃতীয় উপাদানটির বিপরীতে এটি পরীক্ষা করা, যেখানে আমরা আউটপুট ভেরিয়েবল সংরক্ষণ করুন।

এবং সেখানে আমাদের চারটি সীমাবদ্ধতার সাথে আমাদের R1CS আছে। সাক্ষী হল ইনপুট, আউটপুট এবং অভ্যন্তরীণ ভেরিয়েবল সহ সমস্ত ভেরিয়েবলের জন্য বরাদ্দ করা:

[1, 3, 35, 9, 27, 30]

আপনি উপরের সমতল কোডটি "এক্সিকিউট" করে, ইনপুট ভেরিয়েবল অ্যাসাইনমেন্ট �=3 দিয়ে শুরু করে এবং সমস্ত মধ্যবর্তী ভেরিয়েবলের মান এবং আউটপুট হিসাবে গণনা করার মাধ্যমে এটি নিজের জন্য গণনা করতে পারেন।

সম্পূর্ণ R1CS একসাথে রাখা হল:

A
[0, 1, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 0]
[0, 1, 0, 0, 1, 0]
[5, 0, 0, 0, 0, 1]

B
[0, 1, 0, 0, 0, 0]
[0, 1, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]

C
[0, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 1, 0]
[0, 0, 0, 0, 0, 1]
[0, 0, 1, 0, 0, 0]

QAP থেকে R1CS

পরবর্তী পদক্ষেপটি হল এই R1CS গ্রহণ করা এবং এটিকে QAP ফর্মে রূপান্তর করা, যা ডট পণ্যের পরিবর্তে বহুপদ ব্যবহার করা ছাড়া একই যুক্তি প্রয়োগ করে। অনুসরণ হিসাবে আমরা এই কাজ। আমরা তিন ডিগ্রী-৩ বহুপদীর ছয় থেকে ছয়টি দৈর্ঘ্যের তিনটি ভেক্টরের চারটি গ্রুপ থেকে যাই, যেখানে প্রতিটিতে বহুপদী মূল্যায়ন করা হয় x সমন্বয় সীমাবদ্ধতার একটি প্রতিনিধিত্ব করে। অর্থাৎ, যদি আমরা �=1-এ বহুপদকে মূল্যায়ন করি, তাহলে আমরা আমাদের ভেক্টরের প্রথম সেট পাব, যদি আমরা �=2-এ বহুপদকে মূল্যায়ন করি, তাহলে আমরা আমাদের ভেক্টরের দ্বিতীয় সেট পাব, ইত্যাদি।

আমরা একটি নামক কিছু ব্যবহার করে এই রূপান্তর করতে পারি ল্যাগ্রেঞ্জ ইন্টারপোলেশন. একটি ল্যাগ্রেঞ্জ ইন্টারপোলেশন যে সমস্যাটি সমাধান করে তা হল: আপনার যদি বিন্দুগুলির একটি সেট থাকে (অর্থাৎ (�,�) সমন্বয় জোড়া), তাহলে সেই বিন্দুগুলিতে একটি ল্যাগ্রেঞ্জ ইন্টারপোলেশন করলে আপনাকে একটি বহুপদ দেয় যা সেই সমস্ত বিন্দুর মধ্য দিয়ে যায়। আমরা সমস্যাটি পচানোর মাধ্যমে এটি করি: প্রতিটি � স্থানাঙ্কের জন্য, আমরা একটি বহুপদ তৈরি করি যার পছন্দসই � স্থানাঙ্ক রয়েছে � স্থানাঙ্কে এবং একটি � 0 এর স্থানাঙ্ক অন্যান্য সকল � স্থানাঙ্কে আমরা আগ্রহী, এবং তারপর চূড়ান্ত পেতে ফলস্বরূপ আমরা সমস্ত বহুপদী একসাথে যোগ করি।

একটি উদাহরণ করা যাক. ধরুন আমরা একটি বহুপদ চাই যা (1,3), (2,2) এবং (3,4) এর মধ্য দিয়ে যায়। আমরা একটি বহুপদ তৈরি করে শুরু করি যা (1,3), (2,0) এবং (3,0) এর মধ্য দিয়ে যায়। যেহেতু দেখা যাচ্ছে, একটি বহুপদ তৈরি করা যা �=1 তে "স্টিক আউট" এবং আগ্রহের অন্যান্য বিন্দুতে শূন্য; আমরা সহজভাবে করি:

(x - 2) * (x - 3)

যা এই মত দেখায়:

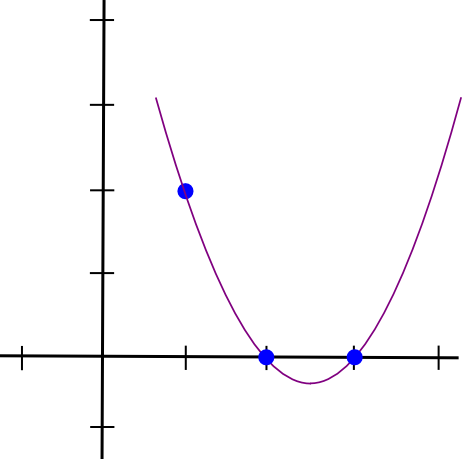
এখন, আমাদের কেবল এটিকে "পুনঃস্কেল" করতে হবে যাতে x=1 এর উচ্চতা সঠিক হয়:

(x - 2) * (x - 3) * 3 / ((1 - 2) * (1 - 3))

এটি আমাদের দেয়:

1.5 * x**2 - 7.5 * x + 9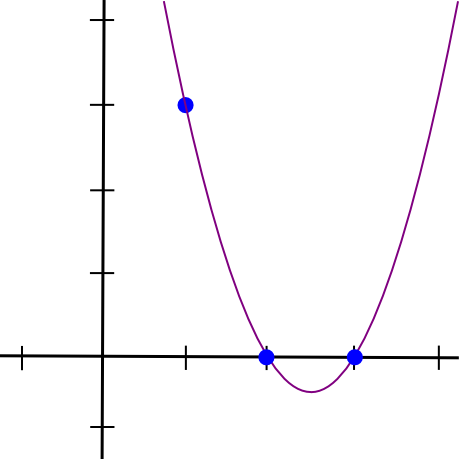

তারপরে আমরা অন্য দুটি বিন্দুর সাথে একই কাজ করি, এবং দুটি একই রকমের বহুপদ পাই, ব্যতীত যে তারা �=2 এর পরিবর্তে �=3 এবং �=1 এ "আউট" থাকে। আমরা তিনটি একসাথে যোগ করি এবং পাই:

1.5 * x**2 - 5.5 * x + 7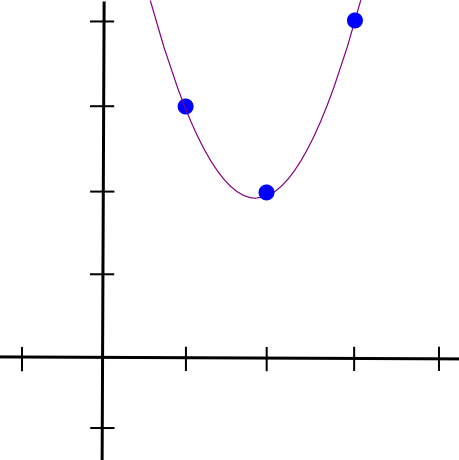

ঠিক যে স্থানাঙ্ক আমরা চাই সঙ্গে. উপরে বর্ণিত অ্যালগরিদমটি �(�3) সময় নেয়, কারণ এখানে � বিন্দু রয়েছে এবং প্রতিটি বিন্দুর বহুপদকে একসাথে গুণ করার জন্য �(�2) সময় প্রয়োজন; একটু চিন্তা করে, এটিকে �(�2) সময় কমানো যেতে পারে, এবং অনেক বেশি চিন্তা করে, দ্রুত ফুরিয়ার ট্রান্সফর্ম অ্যালগরিদম এবং এর মতো ব্যবহার করে, এটি আরও কমানো যেতে পারে — একটি গুরুত্বপূর্ণ অপ্টিমাইজেশান যখন zk-এ ব্যবহৃত ফাংশনগুলি অনুশীলনে SNARK-এর প্রায়ই হাজার হাজার গেট থাকে।

এখন, আমাদের R1CS রূপান্তর করতে Lagrange ইন্টারপোলেশন ব্যবহার করা যাক। আমরা যা করতে যাচ্ছি তা হল প্রতিটি � ভেক্টরের প্রথম মানটি বের করা, ল্যাগ্রেঞ্জ ইন্টারপোলেশন ব্যবহার করে এটি থেকে একটি বহুপদ তৈরি করা (যেখানে � তে বহুপদী মূল্যায়ন করলে আপনি �ম � ভেক্টরের প্রথম মান পাবেন), প্রক্রিয়াটি পুনরাবৃত্তি করুন। প্রতিটি � এবং � ভেক্টরের প্রথম মানের জন্য, এবং তারপর দ্বিতীয় মান, তৃতীয়, মান, ইত্যাদির জন্য সেই প্রক্রিয়াটি পুনরাবৃত্তি করুন। সুবিধার জন্য আমি এখনই উত্তর প্রদান করব:

A polynomials
[-5.0, 9.166, -5.0, 0.833]
[8.0, -11.333, 5.0, -0.666]
[0.0, 0.0, 0.0, 0.0]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]
[-1.0, 1.833, -1.0, 0.166]

B polynomials
[3.0, -5.166, 2.5, -0.333]
[-2.0, 5.166, -2.5, 0.333]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]

C polynomials
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[-1.0, 1.833, -1.0, 0.166]
[4.0, -4.333, 1.5, -0.166]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]

সহগগুলি আরোহী ক্রমে, তাই উপরের প্রথম বহুপদটি আসলে 0.833⋅�3—5⋅�2+9.166⋅�−5। বহুপদীর এই সেটটি (একটি Z বহুপদ যা আমি পরে ব্যাখ্যা করব) এই নির্দিষ্ট QAP উদাহরণের জন্য পরামিতি তৈরি করে। মনে রাখবেন যে এই বিন্দু পর্যন্ত সমস্ত কাজ শুধুমাত্র একবার করতে হবে প্রতিটি ফাংশনের জন্য যা আপনি যাচাই করতে zk-SNARK ব্যবহার করার চেষ্টা করছেন; একবার QAP প্যারামিটার তৈরি হয়ে গেলে, সেগুলি পুনরায় ব্যবহার করা যেতে পারে।

আসুন এই সকল বহুপদকে �=1 এ মূল্যায়ন করার চেষ্টা করি। �=1 তে একটি বহুপদকে মূল্যায়ন করার অর্থ হল সমস্ত সহগ যোগ করা (সকলের জন্য 1�=1 হিসাবে �), তাই এটি কঠিন নয়। আমরা পেতে:

A results at x=1
0
1
0
0
0
0

B results at x=1
0
1
0
0
0
0

C results at x=1
0
0
0
1
0
0

এবং দেখুন এবং দেখুন, আমাদের এখানে যা আছে তা প্রথম লজিক গেটের জন্য তিনটি ভেক্টরের সেটের মতো যা আমরা উপরে তৈরি করেছি।

QAP চেক করা হচ্ছে

এখন এই উন্মাদ রূপান্তর কি লাভ? উত্তর হল R1CS-এর সীমাবদ্ধতাগুলি পৃথকভাবে পরীক্ষা করার পরিবর্তে, আমরা এখন পরীক্ষা করতে পারি একই সময়ে সমস্ত সীমাবদ্ধতা ডট পণ্য চেক করে বহুপদে.

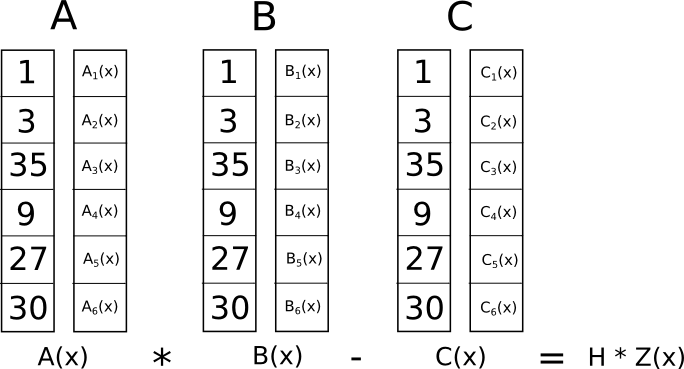
কারণ এই ক্ষেত্রে ডট প্রোডাক্ট চেক হল বহুপদীর সংযোজন এবং গুণের একটি সিরিজ, ফলাফলটি নিজেই একটি বহুপদ হতে চলেছে। যদি ফলিত বহুপদী, প্রতিটি � স্থানাঙ্কে মূল্যায়ন করা হয় যা আমরা একটি লজিক গেটকে উপস্থাপন করার জন্য উপরে ব্যবহার করেছি, শূন্যের সমান হয়, তাহলে এর অর্থ হল সমস্ত চেক পাস হয়; যদি ফলিত বহুপদী মূল্যায়ন করা হয় অন্তত একটি � স্থানাঙ্ক একটি লজিক গেট প্রতিনিধিত্ব করে একটি অশূন্য মান দেয়, তাহলে এর মানে হল যে সেই লজিক গেটের ভিতরে এবং বাইরে যাওয়া মানগুলি অসামঞ্জস্যপূর্ণ (যেমন গেটটি হল �=�⋅�� �1 কিন্তু প্রদত্ত মান হতে পারে �=2,���1=2 এবং �=5)।

উল্লেখ্য যে, ফলস্বরূপ বহুপদকে শূন্য হতে হবে না, এবং আসলে বেশিরভাগ ক্ষেত্রেই হবে না; এটির পয়েন্টগুলিতে এমন কোনও আচরণ থাকতে পারে যা কোনও লজিক গেটের সাথে সঙ্গতিপূর্ণ নয়, যতক্ষণ না ফলাফলটি সমস্ত পয়েন্টে শূন্য হয় do কিছু গেট অনুরূপ. সঠিকতা পরীক্ষা করার জন্য, আমরা আসলে একটি গেটের সাথে সম্পর্কিত প্রতিটি বিন্দুতে বহুপদী �=�.�⋅�.�−�.� মূল্যায়ন করি না; পরিবর্তে, আমরা �কে অন্য বহুপদী দ্বারা ভাগ করি, �, এবং পরীক্ষা করি যে � সমানভাবে ভাগ করে � – অর্থাৎ, বিভাজন �/� কোন অবশিষ্ট থাকে না।

� কে (�−1)⋅(�−2)⋅(�−3)… হিসাবে সংজ্ঞায়িত করা হয়েছে – সবচেয়ে সহজ বহুপদী যা লজিক গেটের সাথে সম্পর্কিত সমস্ত বিন্দুতে শূন্যের সমান। এটি বীজগণিতের একটি প্রাথমিক সত্য যে কোন এই সমস্ত বিন্দুতে শূন্যের সমান বহুপদীকে এই ন্যূনতম বহুপদীর একটি গুণিতক হতে হবে, এবং যদি একটি বহুপদীটি � এর গুণিতক হয় তবে সেই বিন্দুগুলির যেকোনো একটিতে তার মূল্যায়ন হবে শূন্য; এই সমতা আমাদের কাজ অনেক সহজ করে তোলে.

এখন, আসুন আসলে উপরের বহুপদ দিয়ে ডট পণ্য পরীক্ষা করি। প্রথমত, মধ্যবর্তী বহুপদ:

A . s = [43.0, -73.333, 38.5, -5.166]
B . s = [-3.0, 10.333, -5.0, 0.666]
C . s = [-41.0, 71.666, -24.5, 2.833]

এখন, �.�⋅�।�—�।�:

t = [-88.0, 592.666, -1063.777, 805.833, -294.777, 51.5, -3.444]

এখন, ন্যূনতম বহুপদী �=(�−1)⋅(�−2)⋅(�−3)⋅(�−4):

Z = [24, -50, 35, -10, 1]

এবং যদি আমরা উপরের ফলাফলটিকে � দ্বারা ভাগ করি, আমরা পাই:

h = t / Z = [-3.666, 17.055, -3.444]

কোন অবশিষ্ট নেই.

এবং তাই আমরা QAP জন্য সমাধান আছে. যদি আমরা R1CS সলিউশনের যেকোন ভেরিয়েবলকে মিথ্যে করার চেষ্টা করি যেগুলি থেকে আমরা এই QAP সমাধানটি বের করছি — বলুন, শেষটিকে 31-এর পরিবর্তে 30-এ সেট করুন, তাহলে আমরা একটি � বহুপদ পাব যা চেকগুলির একটিতে ব্যর্থ হয় (সেই বিশেষভাবে ক্ষেত্রে, �=3 তে ফলাফল 1 এর পরিবর্তে −0 এর সমান হবে), এবং অধিকন্তু � � এর গুণিতক হবে না; বরং, �/� ভাগ করলে [−5.0,8.833,−4.5,0.666] অবশিষ্ট থাকবে।

উল্লেখ্য যে উপরেরটি একটি সরলীকরণ; "বাস্তব জগতে", যোগ, গুণ, বিয়োগ এবং ভাগ নিয়মিত সংখ্যার সাথে হবে না, বরং সসীম ক্ষেত্রের উপাদানগুলির সাথে ঘটবে - একটি ভুতুড়ে ধরনের গাণিতিক যা স্ব-সংগতিপূর্ণ, তাই সমস্ত বীজগণিতিক নিয়ম আমরা জানি এবং এখনও ভালবাসি সত্য ধরে রাখুন, কিন্তু যেখানে সমস্ত উত্তর কিছু সসীম-আকারের সেটের উপাদান, সাধারণত কিছু � জন্য 0 থেকে �−1 এর মধ্যে পূর্ণসংখ্যা। উদাহরণস্বরূপ, যদি �=13, তাহলে 1/2=7 (এবং 7⋅2=1), 3⋅5=2, এবং আরও অনেক কিছু। সীমিত ক্ষেত্রের গাণিতিক ব্যবহার করে রাউন্ডিং ত্রুটির বিষয়ে উদ্বিগ্ন হওয়ার প্রয়োজনীয়তা দূর করে এবং সিস্টেমটিকে উপবৃত্তাকার বক্ররেখার সাথে সুন্দরভাবে কাজ করার অনুমতি দেয়, যা শেষ পর্যন্ত zk-SNARK যন্ত্রপাতির জন্য প্রয়োজনীয় যা zk-SNARK প্রোটোকলকে প্রকৃতপক্ষে সুরক্ষিত করে তোলে।

আমাকে zk-SNARK-এর অভ্যন্তরীণ কার্যকারিতা সম্পর্কে অনেক বিশদ ব্যাখ্যা করতে সাহায্য করার জন্য Eran Tromer কে বিশেষ ধন্যবাদ।

• এসইও চালিত বিষয়বস্তু এবং পিআর বিতরণ। আজই পরিবর্ধিত পান।
• PlatoData.Network উল্লম্ব জেনারেটিভ Ai. নিজেকে ক্ষমতায়িত করুন। এখানে প্রবেশ করুন.
• প্লেটোএআইস্ট্রিম। Web3 ইন্টেলিজেন্স। জ্ঞান প্রসারিত. এখানে প্রবেশ করুন.
• প্লেটোইএসজি। কার্বন, ক্লিনটেক, শক্তি, পরিবেশ সৌর, বর্জ্য ব্যবস্থাপনা. এখানে প্রবেশ করুন.
• প্লেটো হেলথ। বায়োটেক এবং ক্লিনিক্যাল ট্রায়াল ইন্টেলিজেন্স। এখানে প্রবেশ করুন.
• ব্লকঅফসেট। পরিবেশগত অফসেট মালিকানার আধুনিকীকরণ। এখানে প্রবেশ করুন.
• উত্স: প্লেটো ডেটা ইন্টেলিজেন্স।